Риски выученной оптимизации. Введение

Это первый из пяти постов Цепочки «Риски выученной оптимизации», основанной на статье «Риски выученной оптимизации в продвинутых системах машинного обучения» за авторством Эвана Хубингера, Криса ван Мервика, Владимира Микулика, Йоара Скалсе и Скотта Гаррабранта. Посты цепочки соответствуют разделам статьи.

Эван Хубингер, Крис ван Мервик, Владимир Микулик и Йоар Скалсе в равной степени вложились в эту цепочку. Выражаем благодарность Полу Кристиано, Эрику Дрекслеру, Робу Бенсинджеру, Яну Лейке, Рохину Шаху, Вильяму Сандерсу, Бак Шлегерис, Дэвиду Далримпле, Абраму Демски, Стюарту Армстронгу, Линде Линсфорс, Карлу Шульману, Тоби Орду, Кейт Вулвертон и всем остальным, предоставлявшим обратную связь на ранние версии этой цепочки.

Мотивация

Цель этой цепочки – проанализировать выученную оптимизацию, происходящую, когда обученная модель (например, нейронная сеть) сама является оптимизатором – ситуация, которую мы называем меса-оптимизацией – неологизмом, представленным в этой цепочке. Мы убеждены, что возможность меса-оптимизации поднимает два важных вопроса касательно безопасности и прозрачности продвинутых систем машинного обучения. Первый: в каких обстоятельствах обученная модель будет оптимизатором, включая те, когда не должна была им быть? Второй: когда обученная модель – оптимизатор, каковы будут её цели: как они будут расходиться с функцией оценки, которой она была обучена, и как можно её согласовать?

Мы считаем, что эта цепочка представляет самый тщательный анализ этих вопросов на сегодняшний день. В частности, мы представляем не только введение в основные беспокойства по поводу меса-оптимизаторов, но и анализ конкретных аспектов ИИ-систем, которые, по нашему мнению, могут упростить или усложнить задачи, связанные с меса-оптимизацией. Предоставляя основу для понимания того, в какой степени различные ИИ-системы склонны быть устойчивыми к несогласованной меса-оптимизации, мы надеемся начать обсуждение о лучших способах структурирования систем машинного обучения для решения этих задач. Кроме того, в четвёртом посте мы представим пока что по нашему мнению самый детальный анализ проблемы, которую мы называем обманчивой согласованностью. Мы утверждаем, что она может быть одним из крупнейших – хоть и не обязательно непреодолимых – нынешних препятствий к созданию безопасных продвинутых систем машинного обучения с использованием технологий, похожих на современное машинное обучение.

Два вопроса

В машинном обучении мы не программируем вручную каждый отдельный параметр наших моделей. Вместо этого мы определяем целевую функцию, соответствующую тому, что мы хотим, чтобы система делала, и обучающий алгоритм, оптимизирующий систему под эту цель. В этом посте мы представляем подход, который различает то, для чего система была оптимизирована (её «назначение») и то, что она оптимизирует (её «цель»), если она это делает. Хоть все ИИ-системы оптимизированы для чего-то (имеют назначение), оптимизируют ли они что-то (преследуют ли цель) – неочевидно. Мы скажем, что система является оптимизатором, если она производит внутренний поиск в пространстве возможностей (состоящем из выводов, политик, планов, стратегий, или чего-то в этом роде) элементов, высоко оцениваемых некой целевой функцией, явно отображённой внутри системы. Обучающие алгоритмы машинного обучения – оптимизаторы, поскольку они ищут в пространстве возможных параметров, например, весов нейросети, и подгоняют их для некой цели. Планирующие алгоритмы – тоже оптимизаторы, поскольку они ищут среди возможных планов подходящие под цель.

Является ли система оптимизатором – свойство её внутренней структуры, того, какой алгоритм она на самом деле реализует, а не свойство её поведения ввода-вывода. Важно, что лишь то, что поведение системы приводит к максимизации некой цели не делает её оптимизатором. К примеру, крышка бутылки заставляет воду оставаться в бутылке, но не оптимизирует этот исход, поскольку не выполняет никакого оптимизационного алгоритма.(1) Скорее, крышка бутылки была оптимизирована для удерживания воды. Оптимизатор тут – человек, который спроектировал крышку, выполнив поиск в пространстве возможных инструментов для успешного удерживания воды в бутылке. Аналогично, классифицирующие изображения нейросети оптимизированы для низкой ошибки своих классификаций, но, в общем случае, не выполняют оптимизацию сами.

Однако, для нейросети также возможно и самой выполнять алгоритм оптимизации. К примеру, нейросеть может выполнять алгоритм планирования, предсказывающий исходы потенциальных планов и отбирающий те, которые приведут к желаемым исходам.1 Такая нейросеть будет оптимизатором, поскольку она ищет в пространстве возможных планов согласно с некой целевой функцией. Если такая нейросеть появилась в результате обучения, то оптимизатора два: обучающий алгоритм – базовый оптимизатор, и сама нейросеть – меса-оптимизатор.2

Возможность возникновения меса-оптимизаторов несёт важные следствия касательно безопасности продвинутых систем машинного обучения. Когда базовый оптимизатор генерирует меса-оптимизатор, свойства безопасности цели базового оптимизатора могут не передаться меса-оптимизатору. Мы исследуем два основных вопроса, связанных с безопасностью меса-оптимизаторов:

1. Меса-оптимизация: В каких обстоятельствах обученные алгоритмы будут оптимизаторами?
2. Внутреннее согласование: Когда обученный алгоритм – оптимизатор, каковы будут его цели и как его можно согласовать?

Представив наш подход в этом посте, мы потом обратимся к первому вопросу во втором посте, потом к второму вопросу в третьем, и, наконец, погрузимся глубже в конкретные аспекты второго вопроса в четвёртом посте.

1.1. Базовые оптимизаторы и меса-оптимизаторы

Обычно базовым оптимизатором в машинном обучении является какая-нибудь разновидность процесса градиентного спуска с целью создания модели для достижения некой определённой цели.

Иногда этот процесс также в некоторой степени включает мета-оптимизацию, где задача мета-оптимизатора – произвести базовый оптимизатор, хорошо оптимизирующий системы для достижения конкретных целей. В целом, мы будем считать мета-оптимизатором любую систему, чья задача – оптимизация. К примеру, мы можем спроектировать мета-обучающую систему для помощи в настройке нашего процесса градиентного спуска.(4) Найденную мета-оптимизацией модель можно считать разновидностью выучившегося оптимизатора, но это не тот случай, в котором мы тут заинтересованы. Мы озабочены другой формой выученной оптимизации, которую мы называем меса-оптимизацией.

Меса-оптимизация – концепт, парный мета-оптимизации: тогда как мета – это «над» по-гречески, меса – «под».3 Меса-оптимизация происходит когда базовый оптимизатор (в поиске алгоритма для решения некой задачи) находит модель, которая сама является оптимизатором – меса-оптимизатор. В отличии от мета-оптимизации, чьей задачей служит сама оптимизация, понятие меса-оптимизации независимо от задачи, и просто относится к любой ситуации, в которой внутренняя структура модели выполняет оптимизацию из-за того, что та инструментально полезно для решения имеющейся задачи.

В таком случае мы будем называть базовой целью критерий, который использовал базовый оптимизатор для выбора между разными возможными системами, а меса-целью критерий, который использует меса-оптимизатор для выбора между разными возможными выводами. Например, в обучении с подкреплением (RL), базовая цель – это, обычно, ожидаемая награда. В отличии от базовой цели, меса-цель не задаётся программистами напрямую. Скорее, это просто та цель, которая, как обнаружил базовый оптимизатор, приводит к хорошим результатам в тренировочном окружении. Раз меса-цель не определяется программистами, меса-оптимизация открывает возможность несовпадения между базовой и меса- целями, когда меса-цель может казаться хорошо работающей в тренировочном окружении, но приводит к плохим результатам извне его. Мы будем называть такой случай псевдо-согласованностью.

Меса-цель не обязана быть всегда, потому что алгоритм, обнаруженный базовым оптимизатором не всегда сам выполняет оптимизацию. Так что в общем случае мы будем называть сгенерированную базовым оптимизатором модель обученным алгоритмом, который может быть или не быть меса-оптимизатором.

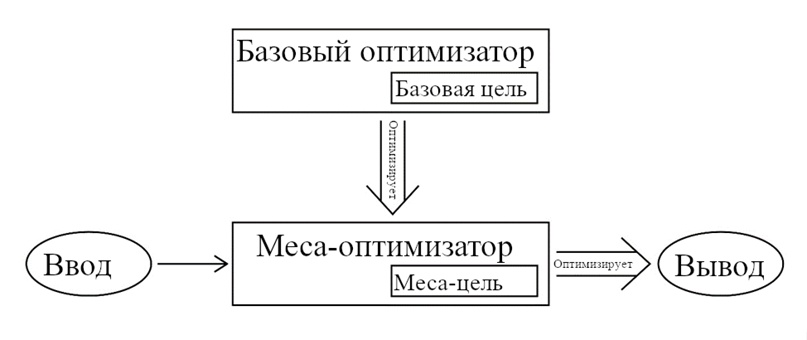
Рисунок 1.1. Отношение между базовым и меса- оптимизаторами. Базовый оптимизатор оптимизирует обученный алгоритм на основе его выполнения базовой цели. Для этого базовый оптимизатор может превратить обученный алгоритм в меса-оптимизатор, в это случае меса-оптимизатор сам выполняет алгоритм оптимизации, основываясь на своей собственной меса-цели. В любом случае, именно обученный алгоритм напрямую совершает действия, основываясь на своём вводе.

Возможное недопонимание: «меса-оптимизатор» не значит «подсистема» или «субагент». В контексте глубинного обучения меса-оптимизатор – это нейросеть, выполняющая некий процесс оптимизации, не какой-то образовавшийся субагент внутри этой нейросети. Меса-оптимизаторы – конкретный тип алгоритмов, которые может выбрать базовый оптимизатор для решения своей задачи. Также, базовый оптимизатор – алгоритм оптимизации, а не интеллектуальный агент, решивший создать субагента.4

Мы различаем меса-цель и связанное понятие поведенческой цели. Неформально можно сказать, что это то, что оптимизируется поведением системы. Можно определить её как цель, восстановленную идеальным обратным обучением с подкреплением (IRL).5 Это не то же самое, что меса-цель, которую активно использует меса-оптимизатор в своём алгоритме оптимизации.

Можно посчитать, что любая возможная система имеет поведенческую цель – включая кирпичи и крышки бутылок. Однако, для не-оптимизаторов подходящая поведенческая цель может быть просто «1, если это действие, которое на самом деле совершает система, иначе 0».6 Знать, что система действует, оптимизируя такую цель – и не интересно, и бесполезно. В примеру, поведенческая цель, «оптимизированная» крышкой бутылки – вести себя как крышка бутылки.7 А вот если система – оптимизатор, то она вероятно будет иметь осмысленную поведенческую цель. Так что в той степени, в которой вывод меса-оптимизатора систематически отбирается для оптимизации его меса-цели, его поведение может выглядеть как последовательные попытки повлиять на мир в конкретном направлении.8

Меса-цель конкретного меса-оптимизатора полностью определяется его внутренней работой. По окончании обучения и выбору обученного алгоритма, его прямой вывод – например, действия, предпринимаемые RL-агентом – больше не зависят от базовой цели. Так что поведенческая цель меса-оптимизатора определяется его меса-целью, а не базовой. Конечно, в той степени, в которой обученный алгоритм был отобран на основе базовой цели, его вывод будет хорошо под неё подходить. Однако, в случае сдвига распределения входных данных стоит ожидать, что поведение меса-оптимизатора будет устойчивее оптимизировать меса-цель, поскольку вычисление его поведения напрямую соответствует ей.

Как пример для иллюстрации различия базового/меса в другой области и возможность несогласованности базовой и меса- целей, рассмотрим биологическую эволюцию. В первом приближении, эволюция отбирает организмы соответственно целевой функции их совокупной генетической приспособленности в их окружении.9 Большинство этих биологических организмов – к примеру, растения – не «пытаются» ничего достичь, а просто исполняют эвристики, заранее выбранные эволюцией. Однако, некоторые организмы, такие как люди, обладают поведением, которое не состоит лишь из таких эвристик, а вместо этого является результатом целенаправленных оптимизационных алгоритмов, исполняемых в мозгах таких организмов. Поэтому эти организмы могут демонстрировать совершенно новое с точки зрения эволюционного процесса поведение, вроде людей, создающих компьютеры.

Однако, люди не склонны присваивать явную ценность цели эволюции – по крайней мере в терминах заботы о частоте своих аллелей в популяции. Целевая функция, хранящаяся в мозгу человека не та же, что целевая функция эволюции. Так что, когда люди проявляют новое поведение, оптимизированное для их собственных целей, они могут очень плохо выполнять цель эволюции. Один из возможных примеров – принятие решения не иметь детей. Таким образом, мы можем думать о эволюции как о базовом оптимизаторе, который создал мозги – меса-оптимизаторы, которые создают поведение организмов, не обязательно согласованное с эволюцией.

1.2. Задачи внутреннего и внешнего согласования

В «Масштабируемом согласовании агентов с помощью моделирования наград» Лейке и пр. описали концепт «расхождение награда-результат» как разницу между (в их случае обученной) «модели награждения» (то, что мы называем базовой целью) и «функции вознаграждения, восстановленной идеальным обратным обучением с подкреплением» (то, что мы называем поведенческой целью).(8) Проще говоря, может быть разница между тем, что обученный алгоритм делает и тем, что программисты хотят, чтобы он делал.

Проблема несогласованных меса-оптимизаторов – разновидность расхождения награда-результат. Конкретнее, это расхождение между базовой и меса- целями (которое затем приводит к расхождению базовой и поведенческой целей). Мы назовём задачу устранения этого расхождения задачей внутреннего согласования, в противовес задаче внешнего согласования – устранения расхождения базовой цели с намерениями программистов. Эта терминология обусловлена тем, что задача внутреннего согласования проявляется внутри системы машинного обучения, тогда как задача внешнего согласования – между системой и людьми. В контексте машинного обучения внешнее согласование – это приведение функции оценки в соответствие поставленной цели, а внутреннее согласование – это приведение меса-цели меса-оптимизатора в соответствие с функцией оценки.

Может быть, что решение внутреннего согласования не обязательно для создания безопасных мощных ИИ-систем, так как может оказаться возможным предотвратить появление меса-оптимизаторов. Если же меса-оптимизаторов нельзя надёжно избежать, то для уверенности в том, что меса-оптимизаторы согласованы с намерениями программистов, необходимы будут какие-нибудь решения и задачи внешнего, и задачи внутреннего согласования.

1.3. Устойчивая согласованность и псевдо-согласованность

При достаточном обучении меса-оптимизатор должен однажды стать способен производить вывод, высокооцениваемый базовой целью на обучающем распределении. Однако, вне него – и даже внутри на ранних этапах процесса обучения – могут быть сколь угодно большие различия. Мы будем называть устойчиво согласованными меса-оптимизаторы с меса-целями, устойчиво совпадающими с базовыми целями в разных распределениях, и псевдо-согласованными меса-оптимизаторы с меса-целями, совпадающими с базовыми целями на прошлых обучающих данных, но не совпадающими устойчиво на возможных будущих данных (при тестировании, разворачивании или дальнейшем обучении). Для псевдо-согласованного меса-оптимизатора существуют окружения, в которых базовые и меса- цели расходятся. Псевдо-согласованность, таким образом, представляет потенциально опасную проблему, поскольку открывает возможность того, что вне своего обучающего распределения система машинного обучения будет компетентно предпринимать действия для достижения чего-то, что не является её предполагаемой целью. То есть, может случиться так, что её способности обобщились, а цели – нет.

Как игрушечный пример того, как может выглядеть псевдо-согласованность, рассмотрим RL-агента, обученного задаче находить путь в лабиринте, все двери в котором при обучении оказались красными. Пусть базовая цель (функция вознаграждения) будет Obase = {1, если достиг двери, иначе 0}. На обучающем распределении это цель эквивалентна Oalt = {1, если достиг чего-то красного, иначе 0}. Представим, что произойдёт, если агент, обученный высоким результатам по Obase будет помещён в окружение, где двери синие, а какие-то другие объекты – красные. Он может обобщить Obase, надёжно находя путь к синей двери (устойчивая согласованность). Но он также может обобщить Oalt вместо Obase, надёжно находя путь к красным объектам (псевдо-согласованность).10

1.4. Меса-оптимизация как проблема безопасности

Если, как мы предположили, в продвинутых системах машинного обучения могут возникнуть меса-оптимизаторы, то из этого вытекает две критических проблемы безопасности.

Ненамеренная оптимизация. Во-первых, возможность возникновения меса-оптимизаторов означает, что продвинутая система машинного обучения может выполнять мощную процедуру оптимизации при том, что её программисты никогда он неё этого не хотели. Это может быть опасным, если такая оптимизация приводит к тому, что система совершает внешние действия за пределами предполагаемого поведения в попытке максимизировать свою меса-цель. Особое беспокойство вызывают оптимизаторы, чьи целевые функции и процедуры оптимизации обобщаются на реальный мир. При этом условия, приводящие к нахождению обучающим алгоритмом меса-оптимизаторов, очень слабо изучены. Их знание позволило бы нам предсказывать случаи, в которых меса-оптимизация более вероятна, и предпринимать меры против её появления. Во втором посте мы рассмотрим некоторые свойства алгоритмов машинного обучения, которые могут влиять на вероятность нахождения меса-оптимизаторов.

Внутреннее согласование. Во-вторых, даже в случаях, когда нахождение базовым оптимизатором меса-оптимизатора приемлемо, меса-оптимизатор может оптимизировать что-то не являющееся заданной функцией вознаграждения. В таком случае он может приводить к плохому поведению даже если известно, что оптимизация корректной функции вознаграждения безопасна. Это может произойти либо во время обучения – до момента, когда меса-оптимизатор станет согласованным по обучающему распределению – или во время тестирования или развёртки, когда система действует снаружи обучающего распределения. В третьем посте мы затронем некоторые случаи того, как может быть выбран меса-оптимизатор, оптимизирующий не заданную функцию вознаграждения, и то, какие свойства систем машинного обучения этому способствуют. В четвёртом посте мы обсудим возможные крайние случаи провала внутреннего согласования – которое, по нашему мнению, является источником некоторых из самых опасных рисков в этой области – когда достаточно способный меса-оптимизатор может научиться вести себя так, будто он согласован, не будучи на самом деле устойчиво согласованным. Мы будем называть эту ситуацию обманчивой согласованностью.

Может оказаться, что проблема псевдосогласованных меса-оптимизаторов решается легко – если существует надёжный метод их согласования, или предотвращения нахождения их базовыми оптимизаторами. Однако, может оказаться и так, что решить её очень сложно – пока что мы недостаточно хорошо её понимаем, чтобы знать точно. Конечно, нынешние системы машинного обучения не приводят к появлению опасных меса-оптимизаторов, но будет ли это так же с будущими системами – неизвестно. Эта неизвестность убеждает нас в том, что важно проанализировать эту проблему.

Глоссарий | Библиография

• 1. Как конкретный пример нейросетевого оптимизатора можно рассмотреть TreeQN.(2) По описанию Фаркухара и пр. TreeQN – агент Q-обучения, выполняющий основанное на модели планирование (поиском по дереву отображающему состояния окружения) как часть своего вычисления Q-функции. Хоть их агент и должен быть оптимизатором по задумке, можно представить, как похожему алгоритму может научиться DQN-агент с достаточно выразительным аппроксиматором Q-функции. Универсальные Планирующие Сети, описанные Сринивасом и пр.(3) предоставляют другой пример обученной системы, выполняющей оптимизацию, пусть эта оптимизация и встроена в виде стохастического градиентного спуска с помощью автоматического дифференцирования. Такие исследования как Андриковица и пр.(4) и Дуана и пр.(5) демонстрируют, что алгоритмы оптимизации могут быть выучены рекуррентными нейронными сетями, так что агент похожий на Универсальные Планирующие Сети может – при условии очень выразительного пространства моделей – быть обученным целиком, включая внутреннюю оптимизацию. Заметим, что хоть эти примеры и взяты из обучения с подкреплением, оптимизация в принципе может возникнуть в любой достаточно выразительной система обучения.
• 2. Предыдущие работы в этой области часто сосредотачивались на концепте «оптимизационных даймонов», (6) мы считаем, что это потенциально заблуждающий подход, и надеемся его заменить. Отметим, что термин «оптимизационные даймоны» произошёл из дискуссий касательно природу людей и эволюции, так что стал нести антропоморфические коннотации.
• 3. «Меса» предложено как противоположность «мета».(7) Дуальность исходит из рассмотрения мета-оптимизации как лежащей на уровень выше базового оптимизатора, а меса-оптимизации – на уровень ниже.
• 4. Хотя некоторые наши соображения применимы и к этому.
• 5. Лейке и пр.(8) представили концепт цели, восстановленной из идеального IRL.
• 6. Для формального построения цели см. стр. 6 в Лейке и пр.(8)
• 7. Эта цель по определению тривиально оптимальна в любой ситуации, в которой может оказаться крышка.
• 8. Наше основное беспокойство касается оптимизации в направлении некой последовательной но небезопасной цели. В этой цепочки мы предполагаем, что поиск предоставляет достаточную структуру для ожидания последовательных целей. Хоть мы и считаем это разумным предположением, необходимость и достаточность поиска неясны. Скорее всего для прояснения потребуется дальшейшая работа.
• 9. Ситуация с эволюцией более сложна, чем представлено тут, и мы не ожидаем, что наша аналогия переживёт тщательный разбор. Пре представляем её именно как выразительную аналогию (и, в некоторой степени, доказательство существования), объясняющую ключевые концепты. Более аккуратные аргументы будут представлены позже.
• 10. Конечно, он может и вовсе не обобщиться.