Написано во время работы в PIBBSS1. Работа началась на грант от Lightspeed Grant и продолжилась в PIBBSS. Написано в сотрудничестве с Полом Рихтерсом, Лукасом Тейшейрой, Александром Гителинком Олдензилем, и Сарой Марзен. Пол обучался в MATS на протяжении некоторой части этой работы. Благодарю Пола, Лукаса, Александра, Сару и Гийома Корлуэра за замечания к посту.

Введение

Какую вычислительную структуру мы встраиваем в LLM, когда обучаем их предсказанию следующего токена? В этом посте мы представляем свидетельство того, что это структура задаётся мета-закономерностями обновления убеждений о скрытых состояниях генерирующего данные процесса. Мы испытываем энтузиазм по поводу этих результатов, потому что:

• У нас есть формализованная связь обучающих данных с внутренней структурой LLM.
• По сути, наши результаты означают, что, продвигаясь по контекстному окну, LLM синхронизируются со своей внутренней моделью мира.
• Ассоциированные с этой синхронизацией вычисления можно формализовать через рамки Вычислительной Механики [от переводчика: это не та же вычислительная механика, которая про физику сплошных сред, но она и в оригинале называется так же]. На её языке можно сказать, что в LLM содержится представление смешанных состояний процесса, который генерирует данные.
• Синхронизационная структура в общем случае богаче самой модели мира. В некотором смысле, LLM выучивают больше, чем модель мира.
• Мы теперь в большей степени надеемся, что можно использовать Вычислительную Механику для интерпретируемости и безопасности ИИ в целом.
• Просто есть что-то крутое само по себе в том, чтобы совершить нетривиальное предсказание (в нашем случае – что в трансформере будет представлена конкретная фрактальная структура) и подтвердить, что оно верно. Если точнее, мы смогли использовать Вычислительную Механику, чтобы совершить априорное и конкретное теоретическое предсказание о геометрии активаций остаточного потока (слева на изображении ниже) и показать, что оно оказалось верным на практике (справа на изображении ниже).

Тут должна быть анимация по этой ссылке. Надпись слева – «Теоретическое предсказание», справа – «Остаточный поток»

Теоретическая база

В этом посте мы представляем, что обучающие данные сгенерированы Скрытой Марковской Моделью (СММ)[^2]. У СММ есть множество скрытых состояний и переходы между ними. Каждому переходу приписано, с какой вероятностью при нём выводится какой токен. Вот несколько примеров СММ и данных, которые они генерируют:

Мы рассматриваем, как связан трансформер с СММ, которая произвела данные, на которых он обучался. Это весьма обобщённо – любой набор данных, который состоит из последовательностей токенов, можно отобразить как сгенерированый СММ. Давайте для теоретической части возьмём простую СММ, которую мы называем Z1R2 («zero one random»). Вот её структура:

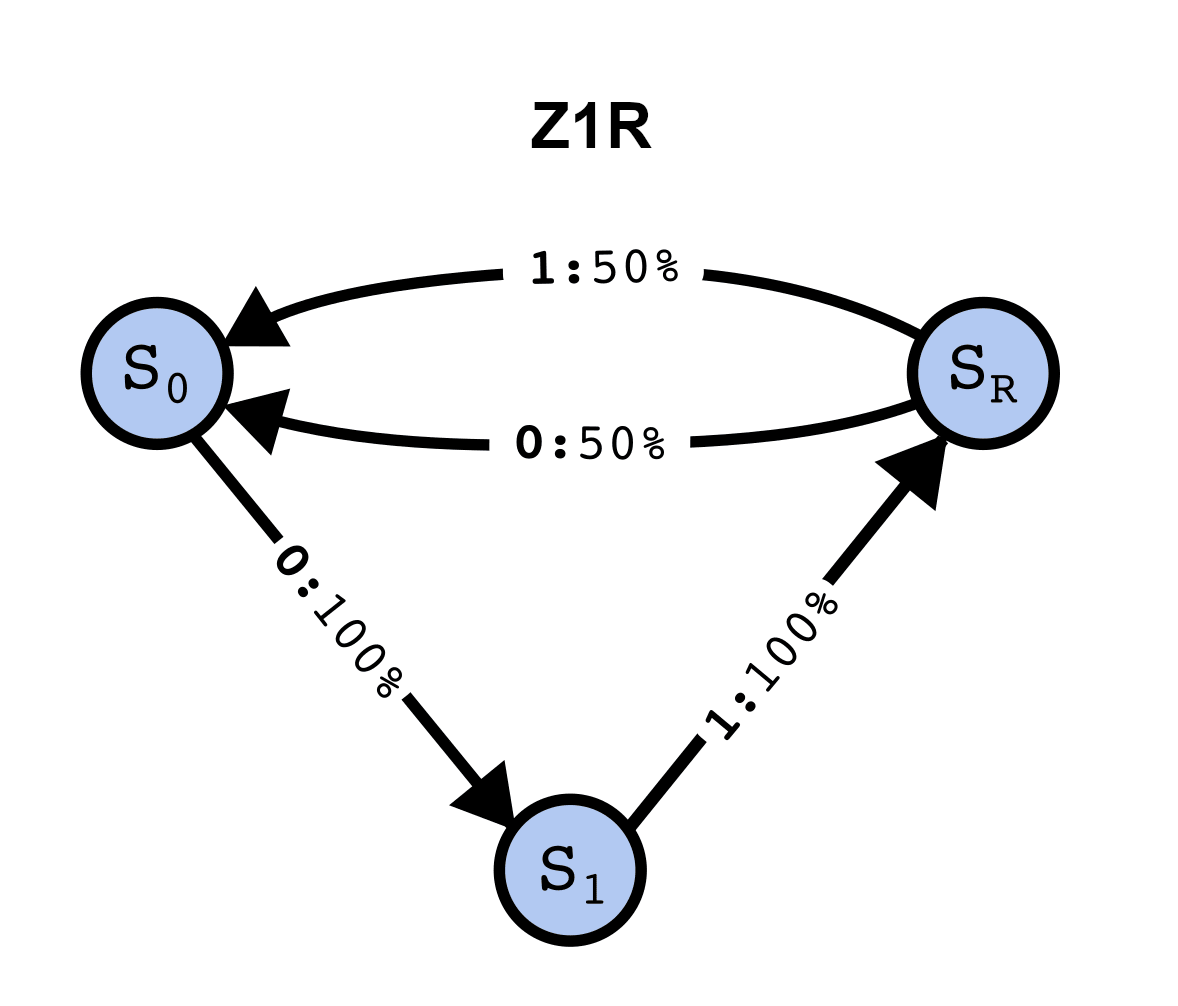
У Z1R три скрытых состояния: S₀, S₁ и S_R. Стрелка из S_x в S_y, над которой написано a:p% означает, что, если процесс находится в состоянии S_x, то вероятность перехода в S_y с выводом токена a равна p%. Таким образом, переходы между состояниями стохастически генерируют бинарную строку вида …01R01R…, где на место R каждый раз случайно с равной вероятностью выбирается 0 или 1.

Структура СММ не выдаётся напрямую данными, которые она сгенерировала. Представьте себе разницу между списком строк, которые выдаёт эта СММ (с приписанными вероятностями) и самой структурой3. У трансформера есть доступ только к строкам, которые выдаёт эта СММ, но не напрямую к информации о скрытых состояниях. Поэтому, чтобы выучить что-то, связанное с скрытой структурой, ему надо вывести её из обучающих данных.

Мы покажем, что когда они хорошо предсказывают следующий токен, трансформеры совершают больше вычислительной работы, чем вывод скрытого генерирующего данные процесса!

Выучивают ли трансформеры модель мира?

Естественное предположение – что трансформеры должны отображать в себе скрытую структуру генерирующего данные процесса (т.е., «мира»4). В нашем случае это были бы три скрытых состояния и вероятностные переходы между ними.

Это предположение часто всплывает (и становится объектом споров) в обсуждениях о то, обладают ли LLM «настоящим пониманием». Например, Илья Суцкевер говорил:

Если подумать об этом, что это значит – достаточно хорошо предсказывать следующий токен? Это на самом деле куда более глубокий вопрос, чем кажется. Хорошее предсказание следующего токена означает, что ты понимаешь реальность, которая лежит в основе, которая привела к появлению этого токена. Это не статистические закономерности. То есть, это статистические закономерности, но что такое статистические закономерности? Чтобы понимать эти закономерности и их сжимать, надо понимать, что это за мир, который создаёт такие закономерности.

Такое представление естественно, но не очень формализовано. Вычислительная Механика – это формализация, которую разработали, чтобы изучать пределы предсказаний хаотичных и других сложных-для-предсказания систем. Она расширилась до глубокой и строгой теории о вычислительных структурах любых процессов. Помимо прочих достижений, она получила строгий ответ на вопрос о том, какие структуры нужны для оптимальных предсказаний. Интересно, что Вычислительная Механика показывает, что предсказание значительно сложнее генерации. Получается, нам следует ожидать, что трансформер, обученный предсказывать следующий токен, должен обладать более сложной структурой, чем процесс генерации данных!

Структура обновления состояния убеждений

Но что это за структура конкретно?

Представим, что вы в точности знаете структуру СММ, которая выдаёт данные вида …01R…. Вы ложитесь спать, потом просыпаетесь и видите, что СММ выдаёт 1. В каком она теперь состоянии? Сгенерировать 1 можно и из детерминированного перехода S₁–>S_r, и из стохастического перехода S_r–>S₀ с вероятностью в 50%. Так как детерминированный переход вдвое вероятнее выдаёт 1, лучшее, что вы можете – это заполучить убеждение-распределение о нынешнем состоянии СММ, в нашем случае это будет P([S₀,S₁,S_R])=[13,0,23]5.

		1	1	0	1…
P(S0)	1/3	1/3	1	0	0
P(S1)	1/3	0	0	1	0…
P(SR)	1/3	2/3	0	0	1…

Пусть после этого вы увидели, как СММ вывела ещё одну 1, так что вместе получается 11. Вы можете взять своё предыдущее убеждение о состоянии СММ (априорное распределение) и своё знание о структуре HMM вместе с выводом, который вы только что видели (соотношение вероятностей), чтобы вычислить новое убеждение (апостериорное распределение). Упражнение для читателя: каким уравнением описывается обновление состояния убеждений, если даны предыдущее состояние убеждений, наблюдаемый токен и матрица перехода СММ, которая выдаёт эти токены?6 В нашем случае есть только один способ, которым СММ может сгенерировать 11 – S₁–>S_R–>S₀, так что вы точно знаете, что СММ теперь в состоянии S₀. С этих пор каждый раз, когда вы будете видеть новый символ, вы будете точно знать, в каком состоянии СММ. Мы будем говорить, что вы синхронизировались с СММ.

В общем случае по мере того, как вы наблюдаете всё больше данных, которые сгенерировала СММ, вы постоянно обновляете своё убеждение о состоянии СММ. Даже в этом простом примере у этих обновлений есть нетривиальная структура. Например, двух выводов не всегда хватает, чтобы синхронизироваться с СММ. Если бы вместо 11… вы увидели 10…, вы бы не синхронизировались, потому что есть два разных способа, которыми СММ могла сгенерировать 10.

Структура обновления убеждений задаётся Представлением Смешанных Состояний.

Представление Смешанных Состояний

Генерирующий данные процесс – СММ – в каждый конкретный момент находится в скрытом состоянии, а затем, выводя символ, переходит в другое скрытое состояние. Заметим, что аналогично ведёт себя и ваше убеждение об этом процессе при условии получения нового вывода. Вы находитесь в некотором состоянии убеждений, а затем, в зависимости от полученного вывода СММ, переходите в некоторое другое состояние убеждений.

	Процесс генерации данных	Процесс обновления убеждений
Состояния принадлежат	Генерирующий данные механизм	Наблюдатель выводов процесса генерации данных
Состояния	Множества последовательностей, определённым образом ограничивающие будущее	Убеждения наблюдателя о состоянии процесса генерации данных
Последовательности скрытых состояний выводят	Разрешённые последовательности токенов	Разрешённые последовательности токенов
Интерпретация вывода	Наблюдения/токены, которые выдаёт процесс генерации данных	Что наблюдатель видит из процесса генерации данных

Мета-закономерности обновления состояний убеждений формально представляют из себя другую СММ, где скрытые состояния – ваши состояния убеждений. Эта мета-структура в Вычислительной Механике называется Представлением Скрытых Состояний (ПСС).

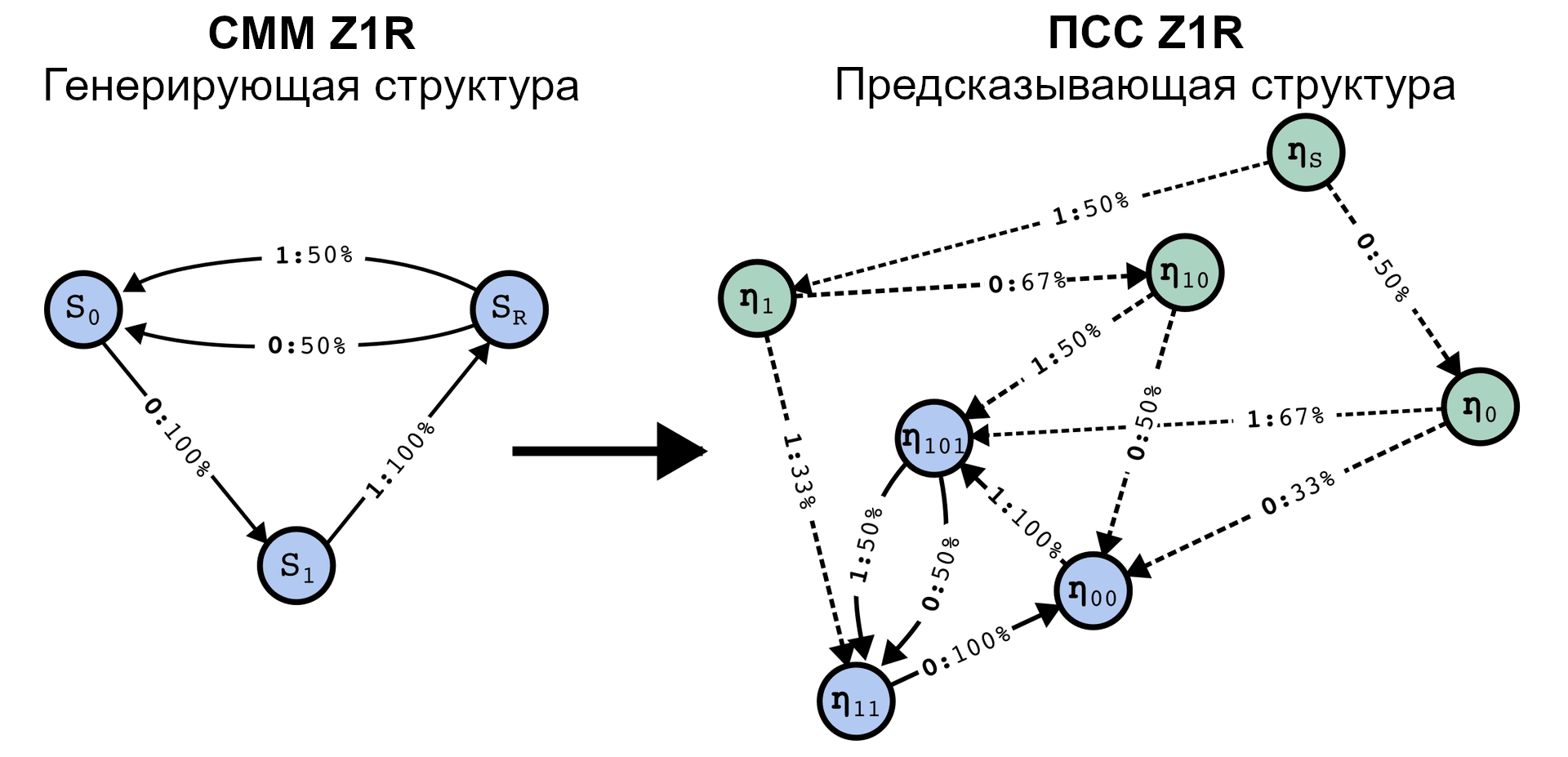
Заметим, что у ПСС есть переходные состояния (выше зелёные), которые ведут к повторяющемуся набору состояний убеждений, изоморфному генерирующему данные процессу. Это всегда так, хотя переходных состояний может быть бесконечно много. Синхронизация – это процесс движения через переходные состояния, сходящийся к генерирующему данные процессу.

Вычислительная Механика учит, что чтобы оптимально предсказывать следующий токен на основании конечной истории вывода токенов, надо реализовать Представление Смешанных Состояний (ПСС). То есть, чтобы хорошо предсказывать следующий токен, надо как можно лучше понимать, в каком состоянии находится генерирующий данные процесс, а для этого нужно ПСС.

С ПСС ассоциировано геометрическое представление, которое получается, если отметить значения состояний убеждений на симплексе. В общем случае, если наш генерирующий данные процесс имеет N состояний, распределения вероятностей на этих состояниях будут иметь N−1 степень свободы, потому что все вероятности должны быть между 0 и 1 [от переводчика: и суммироваться в единицу, это тоже важно, почему-то это не сказали]. Так что все возможные распределения вероятностей лежат на N-1-мерном симплексе. В случае Z1R это 2-симплекс, то есть, треугольник. Мы можем отобразить все возможные состояния на этот 2-симплекс, как показано ниже.

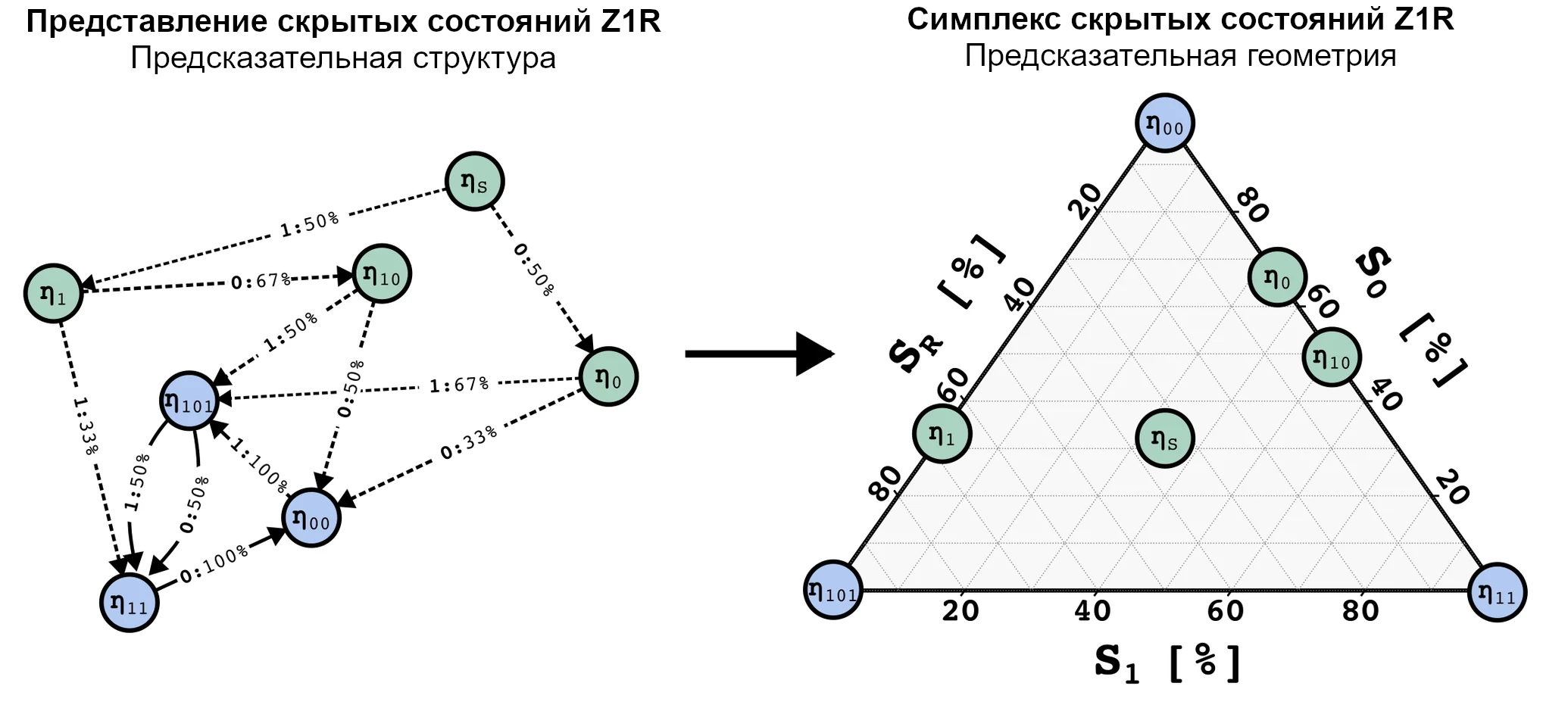
Мы обучили трансформер предсказывать следующий токен данных, сгенерированных СММ с тремя состояниями. Мы смогли найти линейное отображение геометрии ПСС в остаточном потоке. Это удивительно! Заметим, что точки на симплексе, состояния убеждений, это не вероятности, каким будет следующий токен. На самом деле, некоторым точкам тут соответствуют абсолютно одни и те же предсказания следующего токена. В частности, в нашем примере, η₁₀, η_S, and η101 соответствуют одним и тем же оптимальным предсказаниям следующего токена.

Другой способ об этом думать: трансформеры отслеживают различия в ожидаемых распределениях на всё будущее, за пределами различий в предсказании следующего токена, хоть их в явном виде и обучают предсказанию следующего токена! Это означает, что трансформер хранит больше информации, чем необходимо только для локального предсказания следующего токена.

Ещё один способ думать о нашем утверждении: трансформеры совершают два вида рассуждений: одни выводят структуру процесса, который генерирует данные, а другие, мета-рассуждения, обновляют его внутреннее убеждение о том, в каком состоянии этот процесс находится, основываясь на некоторой конечной истории (т.е., контекстном окне).

Последняя теоретическая заметка о Вычислительной Механике и представленной тут теории, так как Вычислительная Механика – хорошо проработанный с чистого листа подход, который не зависит от конкретики архитектуры трансформера, мы можем применить его к любому оптимальному предсказателю, не только трансформерам.7

Эксперимент и результаты

План эксперимента

Повторим вопрос, на который мы пытаемся ответить:

Какую вычислительную структуру мы встраиваем в LLM, обучая их предсказывать следующий токен?

Для проверки наших теоретических предсказаний мы спланировали эксперимент с такими шагами:

1. Сгенерировать обучающий данные при помощи известной СММ, конкретно – СММ из трёх состояний, описанной ниже в разделе «Процесс генерации данных и ПСС».
2. Обучить трансформер предсказанию следующего токена на этих данных. В показанном эксперименте мы использовали трансформер из 4 слоёв с 64-мерным остаточным потоком и 4 «головами внимания» на слой.
3. Проанализировать последний слой остаточного потока трансформера в поисках линейного подпространства, геометрия которого соответствовала бы предсказанной фрактальной структуре Представления Смешанных Состояний (ПСС).

Контроль структуры обучающих данных при помощи использования СММ, позволил нам сделать конкретное фальсифицируемое предсказание о вычислительной структуре, которая должна быть реализована в рассуждениях трансформера. Вычислительная Механика, как описано в разделе «Теоретическая База» выше, даёт способ совершать такие предсказания, основываясь на структуре СММ.

Конкретной СММ, которую мы выбрали, соответствует ПСС с бесконечно-фрактальной геометрией. Это даёт нам весьма нетривиальное предсказание о том, обнаружения чего следует ожидать в активациях остаточного потока трансформера, если наша теория верна.

Процесс генерации данных и ПСС

Для этого эксперимента мы обучили трансформер на данных, сгенерированных простой ПСС под названием Mess3 с всего 3 скрытыми состояниями8. многократные переходы между этими состояниями генерируют строки, состоящие из токенов из множества {A, B, C}. СММ этого процесса изображена слева на рисунке ниже.

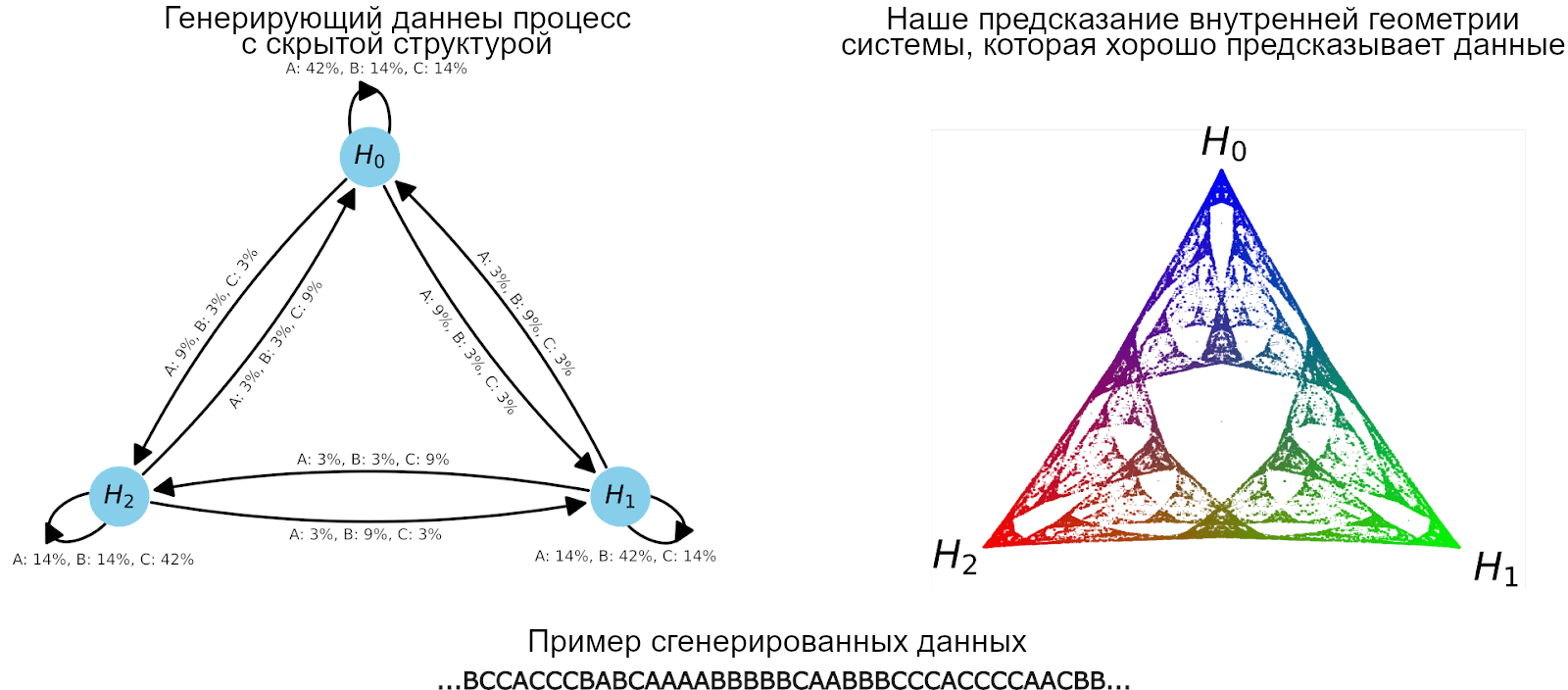
(Слева) Генерирующий данные процесс имеет три скрытых состояния и выводит строки-данные со словарём {A, B, C}. (Снизу) Пути по этой структуре генерируют строки для обучающих данных из токенов, приписанных к рёбрам, по которым эти пути проходят. Мы используем эти данные для обучения на них трансформера. (Справа) Соответствующая Mess3 ПСС – внутренние состояния системы, которая предсказывает будущие токены, которые выдаст генерирующий данные процесс, при условии наблюдения предыдущих токенов. Точки в этом пространстве соответствуют распределениям вероятностей скрытых состояний генерирующего данные процесса. Они лежат на двумерной плоскости, потому что пространство распределений вероятностей трёх вариантов двумерно. Важно, что эта структура – не структура предсказания следующего токена! Это мета-структура того, как обновляются убеждения наблюдателя о скрытых состояниях генерирующего процесса! Центральная точка треугольника соответствует максимальной неуверенности по поводу трёх скрытых состояний, а углы – полной уверенности в одном из них. Цвета присвоены сопоставлением вероятности каждого состояния одного из значений RGB.

Наш подход позволил нам совершить строгое и тестируемое предсказание о внутренней структуре трансформеров. В случае этой СММ, теория (обрисованная выше) заявляет, что обученный на этих данных трансформер должен реализовывать вычислительную структуру, ассоциированную с фрактальной геометрией, показанной справа на рисунке выше. Каждая цветная точка этого симплекса – отдельное состояние убеждений.

Мы выбрали СММ Mess3, потому что его ПСС обладает бесконечной фрактальной структурой, так что может послужить весьма нетривиальным предсказанием о том, какую геометрию мы обнаружим в остаточном потоке.

Результаты!

Мы обучили трансформер на данных, которые сгенерировала Mess3. Мы посмотрели на последний слой остаточного потока и нашли линейное двумерное подпространство, в котором активации обладали весьма похожей на наш предсказанный фрактал структурой. Мы сделали это при помощи обычной линейной регрессии от активаций остаточного потока (64-мерных векторов) к распределениям-убежденям (трёхмерным векторам), которые соответствуют им в ПСС.

(Слева) Наше предсказание внутренней геометрии обученного трансформера, то же, что и на предыдущем рисунке. (Справа) Результаты эксперимента. Мы нашли двумерную линейную проекцию активаций последнего слоя остаточного потока нашего обученного трансформера, геометрия которой схожа с нашим теоретическим предсказанием! Цвета присвоены согласно идеально верному распределению вероятностей (как показано слева).

Можно посмотреть и на то, как эта структура возникает при обучении. Это показывает (1) что найденная структура нетривиальна9, ведь на ранних этапах обучения она не столь подробна, и (2) что происходит постепенная подгонка активаций трансформера к предсказанной нами фрактальной структуре.

По ходу обучения видно оформление внутренних активаций остаточного потока трансформера в фрактальную геометрию, которую предсказал наш подход.

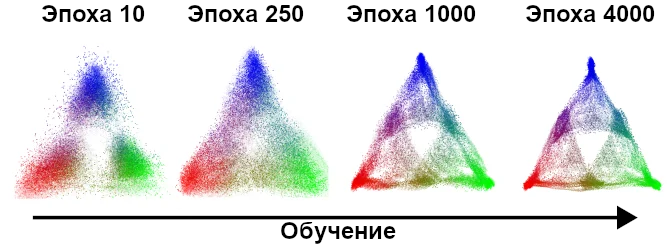
Можно посмотреть визуализацию на этом видео. Для обучения мы использовали стохастический градиентный спуск, поэтому двумерная проекция активаций подрагивает даже после того, как обучение уже сошлось. Можно видеть, что при подрагивании фрактальная структура остаётся.

Ограничения и следующие шаги

Ограничения

• Мы показали одну простую структуру, заданную СММ с тремя состояниями и словарём из трёх токенов. Настоящие современные LLM намного больше и имеют словари больше чем из 50 тысяч токенов, а марковский порядок естественных языков бесконечен. Мы проверяли эту теорию и на других СММ, и всё работало, но пока что это тоже были примерно настолько же маленькие примеры. Как всё это относится к большим, более сложным и более реалистичным ситуациям – неизвестно (но у нас есть мысли по этому поводу!).
• В этом посте мы на этом не сосредотачивались, но МСП – динамическая система, управляемая входными данными (input-driven dynamical system). Для каждого возможного ввода в систему определено, куда в симплексе возможных убеждений надо перейти из какого нынешнего убеждения. Мы не проверяли напрямую, что LLM реализуют эти закономерности, только что в трансформере представлены состояния убеждений и их геометрия.
• Вычислительная Механика в основном говорит об оптимальных предсказаниях. На практике LLM не будут буквально оптимальными. Есть много статей по изучению почти-оптимальности, не-оптимальности и скоростей – искажений (rate-distortion) с точки зрения Вычислительной Механики, но к LLM этого пока не применяли.
• В этой работе мы сфокусировались на эргодических и стационарных процессах. Вычислительная Механика может ослабить эти допущения, но, опять же, мы эти её (очень интересные) расширения не применяли к LLM. В частности, не-эргодичность, скорее всего, лежит в основе обучения в контексте.
• В представленном в этом посте эксперименте мы сосредоточились на последнем слое остаточного потока, прямо перед обращением эмбеддинга. В других (не представленных тут) экспериментах ПСС не была хорошо представлена в последнем слое, а была распределена по нескольким более ранним слоям. Мы думаем, что это происходит, потому что в общем случае есть вырожденные группы состояний убеждений, в том смысле, что у этих состояний одинаковое распределение вероятностей следующего токена. В таком случае, утверждение из этого поста заявляет, что хоть различие между этими состояниями должно быть отображено в внутренней структуре трансформера, но он может затем, двигаясь к предсказанию следующего токена, это различие (локально) потерять. Это в наиболее явном виде происходит прямо перед обращением эмбеддинга.

Следующие шаги

• Мы надеемся, что описанный в этом посте подход даст более формальное понимание внутренней структуры и поведения нейросетей.
• Есть много пока открытых вопросов о том, как эта работа соотносится с другой технической работой по безопасности ИИ. Я очень быстро перечислю несколько идей, а подробнее расскажу о них в будущих постах:
  • Как с геометрией смешанных состояний связаны черты и схемы, которые изучает Механистическая Интерпретируемость?
  • Можно ли что-то сказать о суперпозиции и сжатии ПСС в тех случаях, когда остаточный поток слишком мал, чтобы оно в него «поместилась»?
  • Можно ли связать развитие геометрической структуры ПСС по мере обучения с явлениями из SLT (Singular Learning Theory)? См. К интерпретируемости развития
  • Можно ли использовать наш подход, чтобы операционализировать определённые способности (обучение в контексте, обобщение за пределы распределений, ситуационная осведомлённость, «спящие агенты», и т.д.)? Позволяет ли наш подход изучать их на игрушечных моделях?
  • Можно ли использовать наш подход для понимания структур задач и того, как разные задачи друг с другом связаны? См. [Начальная точка для того, чтобы начать что-то понимать в структурах задач (в машинном обучении)]
• Как уже упоминалось в разделе про ограничения, структуры ПСС в трансформерах распределяются по слоям. Очевидный следующий шаг: изучить, как это происходит и как с этим связана функциональная форма механизма внимания.
• Мы скоро выпустим python-библиотеку для проведения подобных экспериментов. Вот репозиторий на github.
• Вычислительная Механика – хорошо проработанный подход, а этот пост сосредоточен только на малой её части. Мы надеемся применить и другие её аспекты к работе нейросетей и безопасности ИИ, а также расширить её и скомбинировать с другими методами и подходами.
• Если вы хотите узнать больше о Вычислительной Механике, то мы рекомендуем начать с этих статей Шализи и Кратчфилд (2000), Ричерс и Кратчфилд (2018a), и Ричерс и Кратчфилд (2018b)
• Мы (Пол и Адам) собрали средства на открытие новой организации по безопасности ИИ – Simplex! Тут представлена одна малая грань той работы, которую мы надеемся делать, это только начало. Следите за нашими постами, они будут обрисовывать наше более широкое видение на будущее.
• Примерно через месяц мы вместе с Apart проведём хакатон! Мы скоро запостим и об этом. Ещё мы напишем про открытые задачи и предоставим ещё немного ресурсов для экспериментов.
• Впереди ещё много работы! части этого плана исследований лежат на всём диапазоне от чисто математических/теоретических до экспериментальных. Если вы заинтересованы и хотите стать частью этого, пожалуйста, не стесняйтесь с нами связываться!

• 1. В PIBBSS есть вакансии! Я от всего сердца рекомендую их как организацию.
• 2. Если говорить формально, термин процесс относится к распределению вероятностей бесконечных последовательностей токенов, а представление – к конкретной СММ, которая выдаёт строки согласно этому распределению. У процесс бесконечно много представлений.
• 3. Любая СММ определяет распределение вероятностей на бесконечных цепочках выводов.
• 4. Один возможный способ концептуализировать это – считать, что «мир» обладает некоторой (изначально вам неизвестной) скрытой структурой, которая выдаёт наблюдения. Наша задача – вывести скрытую структуру по последовательности наблюдений. Это может быть ради оптимальных предсказаний будущего, а может быть просто потому, что выяснять как работает мир интересно само по себе. Внутри нас есть «модель мира» – внутренняя структура, которая позволяет нам «понимать» скрытую структуру мира. Термин «модель мира» спорный, ничего в посте особо не зависит от этого понятия. Но наша мотивация для этой работы – формализовать интуитивные соображения и аргументы о нейросетях и моделях мира, превратить их в что-то конкретное, а то они часто очень расплывчаты и плохо определены.
• 5. В данном конкретном случае наше изначальное распределение вероятностей – равномерное распределение на трёх состояниях генерирующего данные процесса. Но это не всегда так. В общем случае изначальное распределение задаётся стационарным распределением генерирующей данные СММ.
• 6. Ответ можно найти в разделе IV этой статьи Пола Ричерса.
• 7. В области Вычислительной Механики есть работы, изучающие и неоптимальные или почти-оптимальные предсказания и что с оптимальностью разменивается. Вероятно, это на практике применимо к нейросетям. См. Марзен и Кратчфилд, 2021 и Марзен и Кратчфилд, 2014.
• 8. Этот процесс называется Mess3, он определён в статье Сары Марзен и Джеймса Кратчфилда. В нашей работе мы использовали x=0.05, alpha=0.85.
• 9. Мы провели и контрольный эксперимент, в котором оставили ту же настоящую фрактальную структуру, но перетасовали то, какие вводы соответствуют каким точкам симплекса (этому соответствует перемешивание цветов на графике с правильной структурой). В этом случае, когда мы запустили нашу регрессию, мы получили, что все активации остаточного потока переходили в центральную точку симплекса – центр масс всех точек.