Условная независимость и наивный Байес

Ранее я называл общей информацией $I(X;Y)$ двух переменных $X$ и $Y$ разницу между энтропией составного распределения $H(X,Y)$ и суммарной энтропией частных распределений $H(X) + H(Y)$.

Я приводил пример с переменной $Х$, которая может принимать восемь состояний $X_{1}, …, X_{8}$ (эти состояния при отсутствии каких-либо свидетельств равновероятны) и переменной $Y$, принимающих четыре состояния $Y_{1}, …, Y_{4}$ (также равновероятных при отсутствии каких-либо свидетельств). Можно показать, что предельные энтропии $H(X)$ и $H(Y)$ равны 3 и 2 бита соответственно.

Однако нам известно, что $X$ и $Y$ либо одновременно чётные, либо одновременно нечётные. Таким образом, совместное распределение $(X,Y)$ содержит 16 равновероятных состояний, и энтропия этого распределения равна 4 битам. Это приводит к недостатку энтропии в 1 бит по сравнению с 5 битами $X$ и $Y$, будь они независимыми. Этот недостаток энтропии — общая информация: информация, которую $X$ сообщает нам об $Y$, и наоборот. Это уменьшает нашу неопределенность в знании одной переменной при получении знания о другой.

Но предположим, что существует переменная $Z$ с состояниями «чётно» и «нечётно», с идеальной корреляцией с четностью распределения $(X,Y)$. Иными словами, $Z$ — это просто вопрос: «являются ли $X$ и $Y$ чётными или нечётными?»

Если у нас нет свидетельств об $X$ и $Y$, то, с учётом известной информации, у $Z$ определённо 1 бит энтропии. Есть один бит общей информации между $Z$ и $X$, а также один бит общей информации между $Z$ и $Y$. Сколько получится энтропии у всей системы $(X, Y, Z)$? Можно наивно полагать, что
$$H(X,Y,Z) = H(X) + H(Y) + H(Z) − I(X;Z) − I(Z;Y) − I(X;Y),$$
но, оказывается, это не так.

Составная система $(X, Y, Z)$ обладает 16 возможными состояниями, поскольку $Z$ это лишь вопрос «Являются $X$ и $Y$ четными или нечетными?», поэтому $H(X,Y,Z) = 4$ бита.Но если посчитать согласно вышеприведённой формуле, получится
$$(3 + 2 + 1 − 1 − 1 − 1) бит = 3 бита = Неверно!$$
Почему? Потому что если есть общая информация между $X$ и $Z$, а также общая информация между $Z$ и $Y$, они могут содержать ту же общую информацию, которая появилась бы при подсчёте общей информации между $X$ и $Y$. Например, в нашем случае знание, что $X$ — чётно, приводит к знанию, что $Z$ — чётно, а это в свою очередь говорит нам, что $Y$ — чётно, но это та же самая информация, которую нам даёт $X$ о $Y$. Мы считаем одно и то же два раза, а потому энтропии оказывается слишком мало.

Правильная формула такова:
$$H(X,Y,Z) = H(X) + H(Y) + H(Z) − I(X;Z) − I(Z;Y) − I(X;Y|Z).$$

Последнее слагаемое $I(X;Y|Z)$ означает «информацию, которую $X$ несёт об $Y$, при условии, что $Z$ известно». В нашем случае $X$ не несёт какой-либо информации об $Y$, при условии, что $Z$ известно, поэтому слагаемое равно нулю, а уравнение даёт правильный результат. Ну вот, разве не прекрасно?

«Нет», — правильно ответите вы, — «ведь ты не сказал, как вычислить слагаемое $I(X;Y|Z)$, а лишь словесно описал, что оно должно быть равно нулю».

Мы вычисляем $I(X;Y|Z)$ уже привычным способом. Мы знаем, что $I(X;Y) = H(X) + H(Y) − H(X,Y)$, а поэтому
$$I(X;Y|Z) = H(X|Z) + H(Y|Z) − H(X,Y|Z).$$

А теперь вам должно быть интересно, как вычислить условную энтропию? Исходная формула для энтропии выглядит так:
$$H(S) = -\sum\limits_{i}p(S_{i})\log_{2}{p(S_{i})}$$

Если нам становится известен факт Z0, оставшаяся неопределенность относительно S окажется равна
$$H(S|Z_{0}) = -\sum\limits_{i}p(S_{i}|Z_{0})\log_{2}{p(S_{i}|Z_{0})}.$$

А значит, если нам становится известно что-либо о Z, то в среднем мы ожидаем вот такой неопределенности после этого знания:
$$H(S|Z) = -\sum\limits_{j}\left( p(Z_{j})\sum\limits_{i}p(S_{i}|Z_{j})\log_{2}{p(S_{i}|Z_{j})}\right).$$

Вот так считаются условные энтропии, из которых впоследствии можно извлечь условную общую информацию.

Существует огромное количество вспомогательных теорем вроде
$$H(X|Y) = H(X,Y) − H(Y)$$

и если $I(X;Z) = 0$ и $I(Y;X|Z) = 0$, то $I(X;Y) = 0$,

но я не стану вдаваться в подробности.

«Но», — спросите вы, — «какое отношение это имеет к природе слов и их скрытой байесианской структуре?»

Я несказанно рад вашему вопросу, ведь я собирался рассказать об этом независимо от вашего желания. Но вначале нужно проговорить ещё кое-что.

Следует запомнить — и как следует, — что между общей информацией и байесовским свидетельством есть связь. Общая информация положительна тогда и только тогда, когда вероятность хотя бы одного составного события $P(x,y)$ не равна произведению вероятностей событий по отдельности $P(x)P(y)$. Это, в свою очередь, эквивалентно наличию байесовского свидетельства между $x$ и $y$.

$$I(X;Y) > 0 =>$$
$$P(x,y) \neq P(x) \cdot P(y) $$
$$\frac{P(x,y)}{P(y)} \neq P(x)$$
$$P(x|y) \neq P(x)$$

При условии известного $Z$, уравнения можно переписать как:

$$I(X;Y | Z) > 0 =>$$
$$P(x,y|z) \neq P(x|z) \cdot P(y|z)$$
$$\frac{P(x,y|z)}{P(y|z)} \neq P(x|z)$$
$$\frac{(P(x,y,z) / P(z))}{(P(y, z) / P(z))} \neq P(x|z)$$
$$\frac{P(x,y,z)}{P(y,z)} \neq P(x|z)$$
$$P(x|y,z) \neq P(x|z)$$

Последняя строчка обозначает: «Даже при известном $Z$, знание $Y$ меняет наши представления об $X$»

И, наоборот, в нашем примере знание, что $Z$ чётно или нечётно экранирует $X$ от $Y$. Если мы знаем, что $Z$ — чётно, то информация $Y = Y_{4}$ не помогает нам узнать, в каком именно состоянии находится $X$: $X_{2}$, $X_{4}$, $X_{6}$, или $X_{8}$. Также, если мы знаем, что $Z$ — нечётно, то информация $X = X_{5}$ не несёт информации, находится ли $Y$ в состоянии $Y_{1}$ или $Y_{3}$. Знание $Z$ сделало $X$ и $Y$ условно независимыми.

Условная независимость — очень важное понятие в теории вероятностей. Кто-то даже утверждает, что без условной независимости у вселенной не было бы структуры.

В этом эссе, впрочем, я хочу поговорить лишь об одном виде условной независимости: случае, когда некая центральная переменная экранируется другими окружающими её переменными (получается что-то вроде тела с тентаклями).

Предположим, у нас есть пять переменных $U$, $V$, $W$, $X$ и $Y$, причём для каждой пары этих переменных, одна является свидетельством о другой. То есть, например, если взять пару $U$ и $W$, то знание $U = U_{1}$ изменит ваши убеждения о вероятности $W = W_{1}$.

Что это? Нераспутываемый клубок причин и следствий? Сумасшествие свидетельств? Не обязательно.

Представим, что $U$ — «умеет разговаривать», $V$ — «две руки и десять пальцев», $W$ — «носит одежду», $X$ — «умирает от болиголова», а $Y$ — «красная кровь». Теперь, если вы встретите в повседневной жизни нечто, что может быть яблоком, а может быть и камнем и узнаете, что оно говорит по китайски, вы обязаны присвоить большую вероятность гипотезе, что оно носит одежду. А если вы узнаете, что это нельзя отравить болиголовом, вы присвоите меньшую вероятность гипотезе красной крови.

Некоторые правила строже других. Пауль потерял палец во время извержения вулкана. Младенец Майкл пока не умеет говорить. IRC-бот Ирвин разговаривает, но у него нет крови. Знание о цвете крови, полученное из факта обладания разговорной речью, не экранируется от нас, если мы узнаем, что нечто не носит одежду. Тот, кто не носит одежду и при этом разговаривает, может оказаться нудисткой Нелли.

Этот пример гораздо интереснее, чем, например, случай с пятью целочисленными переменными, которые одновременно чётные или нечётные, но в остальном не связаны друг с другом. В случае с целочисленными переменными знание одной из них экранирует всё, что вторая переменная могла сказать о третьей.

Но в этом новом примере, как показывает случай с нудисткой Нелли, зависимости не исчезают, когда мы узнаём значение одной из переменных. То есть, это всё-таки нераспутываемый клубок причин и следствий?

Не бойтесь! Ведь может существовать шестая переменная $Z$, которая, если бы мы знали её значение, действительно экранировала бы любую пару переменных друг о друга. Может существовать — даже если нам придётся её создать самим, а не наблюдать напрямую — такая переменная, что:

$P(U|V,W,X,Y,Z) = P(U|Z)$
$P(V|U,W,X,Y,Z) = P(V|Z)$
$P(W|U,V,X,Y,Z) = P(W|Z)$
⋮
Возможно, при условии, что нечто является «человеком», вероятности, что оно говорит, носит одежду и обладает стандартным количеством пальцев являются независимыми. У Пауля нет пальца, но у него столько же шансов оказаться нудистом, как и у любого другого человека. Нелли никогда не носит одежду, но это знание не уменьшает вероятности владения ею разговорной речью. А малыш Майкл ещё не говорит, но все конечности у него на месте.

Это называется методом «наивного Байеса». Обычно он не совсем верен, но можно упростить вычисления, если вообразить его истинность. Мы не следим за влиянием ношения одежды на речевые способности, учитывая количество пальцев. Мы просто используем всю наблюдаемую информацию, чтобы оценить вероятность, что перед нами человек (или, наоборот, кто-то ещё — например, шимпанзе или робот). А затем мы применяем наши убеждения о центральном классе, чтобы предсказать то, что мы не наблюдаем: например, уязвимость к болиголову.

Любое наблюдение $U$, $V$, $W$, $X$ или $Y$ лишь является свидетельством переменной центрального класса $Z$, а затем мы используем апостериорное распределение $Z$ для необходимых нам предсказаний ненаблюдаемых переменных $U$, $V$, $W$, $X$ или $Y$.

Знакомо звучит? А должно бы:

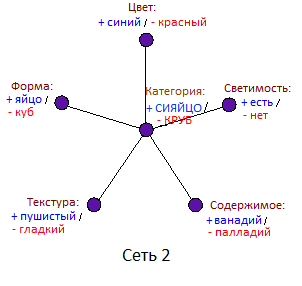
В сущности, если использовать правильные элементы сети, то такая «нейронная сеть» окажется математически эквивалентной наивному Байесу. Нужно лишь, чтобы у центрального элемента была логистическая функция активации, а веса у элементов на входе должны равняться логарифмам соотношений правдоподобия, ну и так далее. Можно даже предположить, что логистическая функция отклика в нейронных сетях так часто подходит в том числе именно потому, что она позволяет алгоритму немножко заниматься байесианскими рассуждениями, пока создатели не смотрят.

Если кто-то показывает вам алгоритм, называя его «нейронной сетью», и прибавляя загадочные слова вроде «неряшливый»1 и «эмерджентный», и при этом гордо заявляет, что невозможно понять, как обученная сеть работает, то не думайте, что этот малыш-ИИ действительно выходит за пределы царства логики. Потому что, в конце концов, если он работает, он окажется байесовой структурой, может даже точь-в-точь алгоритмом, называемым байесовским.

Даже если на первый взгляд он не похож на байесовский.

А потом, как известно, байесианцы начнут объяснять, как этот алгоритм работает, на каких предположениях он основывается, какие зависимости окружающей среды использует, где сработает, а где нет, и даже станут присваивать понятные значения весам натренированной сети.

Досадно, да?

• 1. В оригинале scruffy. — Прим.перев.