Понимание на уровне шестерёнок
Среди бумажных дорожных карт одни полезнее других. Иногда это связано с тем, насколько хорошо карта отражает территорию, однако стоит ещё учитывать и особенности самой карты, не связанные с территорией. Например, линии на карте могут быть жирными и смазанными и из-за этого нельзя разобрать, насколько далеко дорога проходит от реки. Или, скажем, непонятно, какой дороге соответствует какая подпись.
Я хочу показать, что у моделей тоже есть свойство, которое не связано с моделируемым. Оно связано с понятностью моделируемого, но лишь в той же степени, как смазанные линии на дорожной карте связаны с понятностью этой карты.
«Насколько детерминировано сопряжены переменные в модели?» – вот что это за свойство. Я знаю, что есть несколько критериев, которые показывают в какой мере модель обладает данным свойством. Вот далеко не полный список таких критериев:
- Окупается ли модель? Допустим, что она окупается. Если модель будет сфальсифицирована, то сколько (и в какой степени точных) убеждений можно получить из факта её опровержения?
- Насколько нелепо будет предположить, что модель точна, но какая-то из её переменных может принимать иное значение?
- Если модель точна, то можно ли вывести заново позабытое значение одной из переменных?
По-моему, множество разных тем, затронутых на LessWrong, связаны с этим крайне важным свойством. Кроме того, из него можно вывести множество идей и приёмов, но об этом позже.
Я начну с нескольких примеров, а в конце подведу итог и напишу, к чему же всё это.
Пример: шестерёнки в ящике
Взглянем на эти шестерёнки в ящике:

(Рисунок любезно предоставлен моим коллегой, Дунканом Сабиеном.)
Пусть они представляют собой модель внутреннего устройства некой системы из шестерней. Тогда, после поворота левой шестерни против часовой стрелки правая шестерня может повернуться как по ходу движения часовой стрелки, так и против. Созданная таким образом модель не отвечает описанным выше трём критериям:
- Модель не окупается. Допустим ты считал, что правая шестерёнка повернётся в одну сторону, но обнаружил, что она вращается в другую. Единственный вывод, который из этого можно сделать: если схема устройства проста (то есть, ничто не меняет направление вращения правой шестерни исключительно в тех случаях, когда левая шестерня вращается против часовой стрелки), то через направление вращения правой шестерёнки можно узнать, чётно ли количество всех шестерёнок в механизме или нет.
- Правая шестерня легко может вращаться в обе стороны. Твои ожидания ничем не ограничены.
- Ты уже сейчас не знаешь, в какую сторону вращается правая шестерня и не можешь выяснить это.
Представим, что Джо заглядывает внутрь ящика и говорит: «Правая шестерня вращается по часовой». Ты полагаешь, что Джо так скажет скорее в том случае, когда правая шестерёнка вращается по часовой, чем наоборот и это выглядит свидетельством в пользу гипотезы вращения по часовой стрелке. Чем больше людей, подобных Джо, заглядывают в ящик и говорят то же самое, тем больше накапливается свидетельств.
А теперь заглянем внутрь ящика:
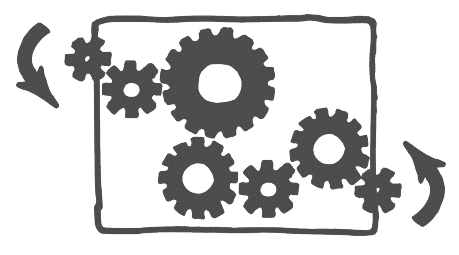
…и теперь мы не понимаем, что же случилось с Джо.
Второй критерий здесь кажется мне особенно важным. Утверждение Джо и очевидная модель не могут быть верны одновременно. И не важно, сколько вообще людей согласны с утверждением Джо. Либо абсолютно все они неправы, либо твоя модель неверна. Логика неуязвима к социальному давлению. То есть, если набрать достаточно свидетельств о том, насколько хорошо твоя карта соответствует данной территории, и эти свидетельства говорят, что твоя карта в целом верна, то у тебя есть весомые эпистемические обоснования пренебречь мнением многих других людей. Собирая свидетельства о соответствии карты и территории ты скорее обнаружишь правду, чем если будешь собирать свидетельства о мнениях других людей.
Любопытно также обратить внимание на первый критерий. Предположим, что правая шестерня и в самом деле крутится по часовой стрелке в том случае, когда левая крутится против часовой. Что из этого следует? Например, из этого следует то, что твоя исходная модель (если я правильно её себе представляю) неверна. Однако она может быть неверна лишь ограниченным количеством способов. Возможно, вторая шестерня слева находится на вертикальной направляющей и, вместо того, чтобы вращаться, движется вверх. Для сравнения: фраза вроде «шестерни работают от волшебства» не даст тебе такой точности.
Объединив эти две идеи, мы переводим взгляд на Джо и замечаем, что можем сформулировать более точные утверждения, чем просто «Джо неправ». Мы знаем, что либо модель шестерней Джо неверна (например, он считает, что какая-то из шестерёнок перемещается по вертикали), либо его модель расплывчата и не так ограничена, как наша (например, он просто сосчитал шестерни и ошибся), либо Джо лжёт. Первые два варианта дают проверяемые предсказания: если его модель неверна, она неверна каким-то конкретным образом; если его модель расплывчата, то должно быть место, где она не удовлетворяет тем трём критериям внутренней связанности моделей. Если во время разговора с Джо мы сконцентрируемся на этих двух возможностях и выяснится, что обе они не соответствуют действительности, то станет ясно, что Джо просто несёт чушь (либо мы не придумали четвёртый вариант).
Благодаря этому примеру у нас в CFAR появился термин: «шестерёночная модель» или «модель на основе шестерёнок». Когда мы подмечаем взаимосвязь, мы говорим о «поиске шестерёнок». Я буду использовать этот термин и дальше.
Пример: арифметика
При сложении 25 и 18 столбиком нужно перенести 1 в разряд десятков. Обычно при этом пишут единицу над двойкой в числе 251.
Забавно то, что можно складывать числа столбиком, совершенно не понимая, что означает эта единица над двойкой и по какой причине её надо ставить.
На самом деле, это достаточно важная проблема при обучении математике. На практике есть расхождение между тем, чтобы (а) запомнить и отработать алгоритмы, которые позволяют быстро вычислять ответы, и (б) «по-настоящему понять» как именно работают эти алгоритмы.
Увы, в сфере образования люди часто устраивают философские дебаты о том, что значит «понимать», и меня это довольно сильно раздражает. Обычно эти споры выглядят так:
- Некто А: Ученики говорят, что они переносят 1, потому что им так сказал учитель. Значит, они не понимают алгоритм сложения по-настоящему.
- Некто Б: Что имеешь в виду под «по-настоящему понимают»? А что не так с тем, чтобы просто следовать инструкции, полученной от человека, который разбирается в предмете?
- А: Но получается, это поведение обосновано социальными, а не математическим причинами.
- Б: Математическое обоснование социально. Формы доказательств, используемые топологами, не будут приняты аналитиками. Что именно в математике будет считаться «доказательством» или «обоснованием» оговаривается социально.
- А: Да ладно. Мы не можем просто договориться, что $e = 3$2, и объявить это истиной. Возможно, способ, которым мы обсуждаем математику является социальным конструктом, но говорим-то мы о чём-то реальном.
- Б: Я не уверен, что это так. И даже если это на самом деле так, то как вы можете понять, что говорите о «чем-то реальном», а не об одном из социальных конструктов, которыми мы пользуемся, чтобы делиться своими мнениями?
И так далее.
(Хотел бы я, чтобы такие споры проходили в атмосфере совместного поиска истины. К сожалению, научное сообщество этого не ценит, поэтому вряд ли я этого дождусь.)
Мне кажется, А пытается указать на то, что у таких учеников модель алгоритма сложения столбиком не шестерёночная (и явно было бы лучше, если бы она стала таковой). Полагаю, что это проясняет и то, что что говорит А, и почему это так важно. Сверимся с нашими критериями:
- Алгоритм сложения столбиком определённо окупается. Например, если отсчитать 25 жетонов, а потом ещё 18, а зачем подсчитать общее их число, то оно должно соответствовать тому, что предсказано алгоритмом. Если же оказалось, что это число не совпадает с количеством подсчитанных жетонов, то ученик может придти лишь к выводу, что алгоритм сложения столбиком не работает для жетонов и больше ничего. (Напротив, если бы я попал в такую ситуацию, то подумал бы, что я либо ошибся в алгоритме, либо ошибся в подсчёте, и был бы весьма уверен, что хотя бы одна из этих двух причин верна.)
- Ученик, наверное, легко может представить себе мир, в котором алгоритм работает и без переноса 1. Это значит, что его модель — во всяком случае, в том виде, как мы её представляем — недостаточно ограничена. (Мой же мозг взрывается при попытке представить, как можно получить правильный ответ, если перенос единицы будет ошибкой.)
- Мы ожидаем, что если ученики забудут указания учителя на случай, когда сумма превышает 9, то они самостоятельно не осознают необходимости перенести единицу в следующий разряд. (Если бы я и забыл о правиле переноса, то я был бы озадачен этим лишним десятком и придумал что-нибудь математически эквивалентное «переносу 1».)
Кажется, в этом контексте полезно табуировать слово «понимать».
Пример: моя мать
Моя мать очень любит изучать историю.
Прямо сейчас, это, вероятно, несвязанный ни с чем случайный факт в твоей голове. Если через месяц я спрошу тебя: «Нравится ли моей матери изучать историю?», ты можешь попытаться вспомнить ответ но с тем же успехом можешь решить, что мир устроен по-другому.
Но только не в моём случае. Если я забуду, как именно мама относится к изучению истории, то я смогу сделать разумное предположение, основанное на общей интуиции. Если я вдруг узнаю, что она не любит историю, это вряд ли окажется для меня крушением основ; в то же время я буду всерьёз озадачен, и задумаюсь, верна ли моя интуиция по поводу того, почему мама увлечена растениями и почему ей нравится общаться с семьёй. Я задумаюсь о том, что недостаточно хорошо понимаю, что за человек моя мать.
Как можно заметить, это применение критериев 1 и 3. При этом, моя модель моей матери не полностью шестерёночна. Я не могу сказать, что она чувствует прямо сейчас или какое из определений деления3 ей ближе. Но критерии показывают, что моя модель моей матери шестерёночнее твоей модели.
Этим примером я хочу подчеркнуть, что свойство «шестерёночности» у моделей небинарно. Это скорее характеристика в диапазоне от «набор случайных поверхностных бессвязных фактов» до «четкой формальной системы с выверенными логическими умозаключениями». (По-крайней мере, так я сейчас представляю себе этот диапазон.)
Кроме того, я считаю, что «узнать» человека как раз и означает повысить шестерёночность своей модели этого человека. «Узнать» человека — это не запомнить несколько разрозненных фактов о том, где он работает, сколько у него детей и чем он увлекается. «Узнать» человека — это значит уточнить степень своего искреннего удивления при получении нового факта, который не вписывается в уже имеющуюся модель твоего знакомого.
(А вот то, насколько твоя шестерёночная модель на самом деле подходит кому-то, кого ты знаешь — это уже вопрос эмпирического характера и относится он к соответствию карты и территории. Сейчас я бы хотел сосредоточиться только на свойствах карт.)
Я считаю, что такие едва шестерёночные модели позволяют нам предполагать, что именно ведущий популярной детской телепередачи4 думает про тех людей, которые издеваются над кошками в Хэллуоин, даже если он никогда не упоминал эту тему. Исходя из критерия №2, вероятно, ты будешь весьма потрясён, если получишь веские свидетельства в пользу того, что он оказался одним из таких людей, и скорее всего, таких свидетельств потребуется действительно много. Согласно критерию №1 тебе потребуется обновить большое количество своих убеждений об этом человеке. Предполагаю, что многие пережили что-то вроде «Да кто же он такой на самом деле?!», когда против Билла Косби выдвинули множество обвинений в совершении преступления5.
Пример: гироскопы
Наблюдая поведение гироскопа большинство людей невольно удивляются. Даже если они логически знают, что подвешенный гироскоп не упадёт, а станет вращаться, то они обычно всё-таки чувствуют, что это как-то странно. Даже те, кто интуитивно понял работу гироскопов, поначалу привыкали к этому и, скорее всего, считали гироскопы удивительными и контринтуитивными.
Как ни странно, для большинства людей допустимо представить себе мир, в котором физика работает точно так же, как в нашем, и только подвешенные за один конец гироскопы сначала падают, а после продолжают вращаться.
Если вы из таких людей, это значит что ваша физическая модель гироскопов не удовлетворяет второму критерию шестерёночности.
Истинная причина, по которой гироскопы ведут себя именно так, как они себя ведут, выводится из трёх законов Ньютона. Представим модель вращения, где а) исполняются три закона Ньютона, и б) подвешенный за один конец гироскоп не вращается, а падает — такая модель не будет согласованной. И если а) и б) кажутся тебе допустимыми одновременно, в твоей модели вращения не хватает шестерёнок.
Вот что привлекает меня в физике — вообще всё состоит из шестерёнок. По-моему, физика — это система шестерёнок, которая возникает при наблюдении за поведением любого физического объекта, вопрошании «Почему он ведёт себя так?» и поиске подходящих шестерёнок. Хотя этот уровнь абстрации и отличается от «шестерёнок людей», но мы ожидаем(по-крайней мере, теоретически), что по мере развития физики удастся соединить шестерёнки механики с шестерёнками, движущими романтическими отношениями.
Хочу сразу пояснить, я не утверждаю, что мир сделан из шестерёнок — такое утверждение содержит ошибку типизации. Как я считаю, суть в самом свойстве шестерёночности, которое позволяет строить более полезные модели — чем модель шестерёночнее, тем больше истины она позволяет узнать о мире.
Шестерёночность это ещё не всё
Подчеркну, что хотя я и считаю, что при прочих равных, чем больше шестерёнок, тем лучше, у моделей есть и другие важные свойства.
Самое очевидное из них — это точность. Большую часть этого эссе я его умышленно игнорировал. Именно для этого свойства крайне важна добродетель эмпиризма. Я же здесь эмпиризм игнорировал, но надеюсь, что не противоречил ему.
Другое важное свойство — генеративность. Приводит ли модель к получению полезного опыта (что бы не значило слово «полезный» в этом контексте)? К примеру, многие воззрения о Боге, божественном или других подобных вещах слишком абстрактны, чтобы окупаться. Однако некоторые люди всё же считают их полезными для переосмысления эмоционального восприятия красоты, смыслов и других людей. Я знаю несколько бывших атеистов, которые считают, что благодаря принятию христианства сделались гораздо более приятными людьми и наладили личные отношения. С эпистемической точки зрения тут есть чего опасаться — религиозный способ мышления проникает в утверждения о реальном устройстве мира. Но если ты эпистемически осторожен, то, возможно, стоит изучить, как использовать силу веры без эпистемологического ущерба.
Так же я считаю, что применение модели имеет смысл даже при нехватке в ней шестерёнок. На самом деле, во многих ситуациях у нас просто нет другого выбора — подавляющее большинство наших моделей не получается полностью связать с физикой. Например, я хотел бы подарить матери некую книгу, поскольку считаю, что она ей понравится; однако в рамках моей модели я могу придумать вариант, почему книга ей может оказаться не интересна. Да, моя модель матери ограничена довольно слабо, но я не считаю, что из-за этого (а) я не должен использовать эту модель или (б) не следует изучать, «почему» я могу оказаться прав и не прав. (Я отношусь к этому, как к предварительным вычислениям: каким бы не оказался мир, мои модели становятся более «чёткими», в них появляется больше шестерёнок. Просто так получается, что я заранее знаю, где они появятся.)
Я это упоминаю, потому что, кажется, зачастую в рационалистских кругах считают, что не стоит обсуждать модели, в которых не хватает шестерёнок. Я против такого подхода. Конечно, я считаю, что очень важно следить за шестерёночностью твоей модели, а не замечать нехватку шестерёнок так и просто просто эпистемически опасно. Очень полезно уметь отличать, хотя бы для себя, в какой модели есть шестерёнки, а в какой — нет. Однако я думаю, что, когда мы пытаемся выстроить правильную эпистемологию, есть и другие качества, не менее важные.
Я бы хотел, чтобы мы помнили о причине, по которой шестёрнки ценны на самом деле, а не зацикливались на шестерёночности самой по себе.
Что дальше
Я считаю, что концепция «шестерёнки в моделях» очень помогает продираться через непонятное. Она защищает наше понимание мира от социальной глупости и требует некоторой строгости мышления, которая, на мой взгляд, объединяет многие идеи в Цепочках.
Я собираюсь развивать эту концепцию и дальше вместе с другими идеями. В частности, я ещё не говорил откуда мы вообще знаем, что шестерёнки достойны внимания. Поэтому, хоть я и рассматриваю шестерёнки как мощное оружие в нашей войне против низкого уровня здравомыслия6, я полагаю, что важно изучить кузницу, в котором оно ковалось. Возможно, это не будет моим следующим постом, но, надеюсь, одним из ближайших.
- 1. В России, насколько я понимаю, часто просто ставят точку. — Прим. перев.
- 2. Основание натурального логарифма, математическая константа приблизительно равная 2,71828 — Прим. перев.
- 3. В оригинале используется оборот «Partitive and Quotitive Division». Точный русский аналог пока найти не удалось. Речь о том, что операцию деления можно определять по разному. Например, когда мы делим 12 на 3, это может означать, что мы хотим делим 12 объектов на 3 части и хотим узнать, сколько объектов в каждой части. Или это может означать, что мы хотим узнать, сколько частей по 3 объекта получится из 12 объектов. — Прим.перев.
- 4. В оригинале Mr. Rogers. — Прим.перев.
- 5. Билл Косби — американский актёр, долгое время лидировавший в индексах общественного одобрения рекламной индустрии, был одним из самых узнаваемых и убедительных рекламных лиц. — Прим. перев.
- 6. Не переведено дословно: «низкого уровня здравомыслия» - в оригинале «sanity drought», дословно «засуха здравомыслия», игра слов с названием эссе Юдковского «Raising the Sanity Waterline». — Прим. перев.