Условная вероятность
Условная вероятность Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle {P}(X\mid Y)} читается как «Вероятность Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle X} с учетом Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle Y} ». Что означает «Вероятность что Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle X} истинно, с учетом что Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle Y} истинно».
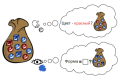
P(желтый|банан) — вероятность того, что банан желтый. Если мы знаем, что это банан, то какова вероятность того, что он желтого цвета?
P(банан|желтый) — вероятность того, что желтая штука — это банан. То есть если в правой стороне написано желтый, то мы задаем вопрос относительно левой стороны: «какова вероятность что банан»?
Понимать формулы условных вероятностей и не путать P(желтый|банан) и P(банан|желтый) важно для понимания терминов отношение правдоподобия и свидетельство.
Содержание
Определение[править]
Для вычисления Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P(left \mid right)} мы сосредоточиваем внимание лишь на тех случаях, когда Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle right} истинно, и интересуемся случаями внутри Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle right} , где Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle left} тоже истинно.
Предположим, что Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle X \wedge Y} читается как «Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle X} и Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle Y} » или же «Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle X} и Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle Y} оба истинны». Тогда Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P(left \mid right) = \dfrac{\mathbb P(left \wedge right)}{\mathbb P(right)}} . Можно рассматривать это, как если бы мы «приближали» лишь случаи, где Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle right} истинно, и спрашивали бы «внутри» этого мира, в каких случаях «Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle right} и Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle left} оба истинны».
Пример 1 — красные и синие объекты[править]
Предположим, что у вас есть мешок с объектами, которые либо красные либо синие, либо круглые либо квадратные. Их количество задается таблицей:
| красные (red) | синие (blue) | |
|---|---|---|
| Квадратные (Square) | 1 | 2 |
| Круглые (Round) | 3 | 4 |
Если вы, засунули руку в мешок, нащупали круглый объект, то условная вероятность того, что он красный, определяется с помощью приближения лишь круглых объектов, и вопроса о частоте объектов одновременно красных и круглых внутри приближенного пространства: Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P(red\mid round) = \dfrac{\mathbb P(red \wedge round)}{\mathbb P(round)} = \dfrac{3}{3 + 4} = \dfrac{3}{7}}
Если вы заглянули в мешок и увидели сверху синий объект, но не разглядели форму, то вычислить условную вероятность того, что он квадратный можно: Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P(square\mid blue) = \dfrac{\mathbb P(square \wedge blue)}{\mathbb P(blue)} = \dfrac{2}{2 + 4} = \dfrac{1}{3}}
Пример 2 — рыжий волос[править]
Предположим, что вы — Шерлок Холмс, расследующий дело об убийстве и на месте преступления вы нашли рыжий волос.
Ведущий это дело детектив Скотланд Ярда говорит: «Ага! Это сделала мисс Скарлет. У нее рыжие волосы, так что если это она убила, то наверняка остался бы рыжий волос. Р(рыжий|Скарлет)=99 %, что позволяет нам почти абсолютную уверенность, так что тут мы, считай, закончили».
"Погодите, " отвечает Холмс, «видите ли, вы некорректно интерпретируете отношения условных вероятностей, детектив. Для изменения нашей уверенности нам нужно не Р(рыжий|Скарлет), то есть шанс, с которым у мисс Скарлет можно обнаружить рыжий волос, но Р(Скарлет|рыжий), то есть шанс с которым рыжий волос будет оставлен именно Скарлет. В городе есть и другие люди, у которых вполне возможно рыжие волосы».
«Значит вы утверждаете…» — медленно произнес детектив, «что Р(рыжий|Скарлет) намного меньше чем 1?»
«Нет же, детектив. Я говорю, что из того что вероятность Р(рыжий|Скарлет) высока, не следует что Р(Скарлет|рыжий) так же высока. Именно вторая и является предметом нашего интереса: как мы, зная о рыжем волосе на месте преступления, выводим, что убийца — мисс Скарлет. И это значение отличается от того, как мы, предполагая что убийца — мисс Скарлет, выводим, что она оставила рыжий волос».
«Но не могут же эти вероятности быть совершенно несвязанными?»
«Ну, а для этого и нужна Теорема Байеса».
Пример 3 — слизеринцы и темные волшебники[править]
— В любом случае, — быстро перебил Драко, — это не имеет отношения к делу, мистер Хагрид. Хотя… — Драко задумался, пытаясь перевести разницу между вероятностью для слизеринца стать Тёмным и вероятностью Тёмного оказаться слизеринцем на ненаучный язык. — Хотя большинство Тёмных волшебников — слизеринцы, лишь немногие из слизеринцев — Тёмные волшебники. А поскольку Тёмных волшебников не так уж и много, ими не могут быть все слизеринцы, — или, как говорил отец, любой Малфой, безусловно, должен владеть многими из тайных искусств, но наиболее… затратные ритуалы лучше оставить полезным глупцам вроде Амикуса Кэрроу.
— Так ты гришь, — произнёс Хагрид, — что большинство Тёмных волшебников — слизеринцы… но…
— Но большинство слизеринцев — не Тёмные волшебники, — закончил Драко. У него появилось нехорошее предчувствие, что на этой части объяснения они застрянут, но, как и в сражении с гидрой, главным было не сдаваться.
Гарри Поттер и методы рационального мышления Глава 100. Меры предосторожности. Часть 1