Шансы
Содержание
Шансы: введение[править]
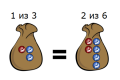
Предположим, что у нас есть мешок, в котором лежат красные и синие шарики, но синих шариков в два раза больше, чем красных. Тогда, если вы достанете не глядя шарик, то шансы Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 2 : 1} в пользу того, что вы вытащили синий.
Шансы выражают относительные количества. Шансы Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 2 : 1} точно такие же как и Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 4 : 2} , как и Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 600 : 300.} Например, если в мешке Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 1} красный шарик и Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 2} синих, или Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 2} красных и Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 4} синих, ваши шансы на то, чтобы вытащить красный шарик одинаковы в обоих случаях:
Другими словами, с учетом шансов Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle (x : y)} , мы можем увеличить их любым положительным числом Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \alpha} и получить эквивалентные шансы Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle (\alpha x : \alpha y).}
Преобразование шансов в вероятности[править]
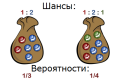
Если в мешке еще есть и зеленые шарики, тогда относительные шансы для красных и синих все еще будут Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle (1 : 2),} но вероятность вытащить красный шарик будет уже ниже.
Если красные (red), синие (blue) и зеленые (green) шарики — составляют все разнообразие шариков в мешке, то мы можем преобразовать шансы Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle (r : b : g)} в вероятности Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle (p_r : p_b : p_g)} с которыми можно вытащить шарик определенного цвета из мешка. Из-за того, что шариков другого цвета в мешке нет, Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle (p_r + p_g + p_b)} будет равняться 1, так что Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle (p_r : p_b : p_g)} будут эквивалентны Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle (r : b : g)} , но «нормализированы» так, чтобы давать в сумме 1. Например, Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle (1 : 2 : 1)} будут нормализироваться в Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \frac{1}{4} : \frac{2}{4} : \frac{1}{4},} что будет соответствовать вероятности вытащить красный/синий/зеленый шарик из мешка.
Отметим, что если красные и синие шарики не составляют все возможные варианты, то особого смысла в преобразовании шансов Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle (r : b)} в вероятности нет. Например, если у нас в мешке Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 100} зеленых шариков, Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 1} красный и Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 2} синих, тогда соотношение красных к синим будет все еще Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 1 : 2} , но вероятность вытащить красный шарик будет намного ниже Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \frac{1}{3}} . Преобразовывать шансы в вероятности можно лишь когда возможные варианты взаимоисключающие и исчерпывающие.
Представьте лес, где часть деревьев больна, а часть здорова, и шансы на то, что дерево больно составляют Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle (2 : 3)} , и каждое дерево либо больно, либо здорово. В таком случае вероятность того, что случайно выбранное дерево из всех в лесу окажется больным составляет Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \frac{2}{5}} , потому что Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 2} из каждых Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle (2+3)} деревьев больны.
В целом, выполняемая нами операция такая: мы берем относительные шансы вроде Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle (a : b : c \ldots)} и делим каждую переменную на их сумму Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle (a + b + c \ldots)} и получаем Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \left(\frac{a}{a + b + c \ldots} : \frac{b}{a + b + c \ldots} : \frac{c}{a + b + c \ldots}\ldots\right)} . Деление каждой переменной на их сумму дает нам эквивалентный набор шансов (потому что каждая переменная делится на одно и то же число), но при этом дающий в сумме 1.
Этот процесс деления набора шансов на сумму их переменных для получения набора вероятностей, дающих в сумме 1, называется нормализацией.
Преобразование вероятностей в шансы[править]
Предположим, что у нас есть два события Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle R} и Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle B} , которые могут представлять вещи вроде «я вытаскиваю красный шарик» и «я вытаскиваю синий шарик». Предположим, Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathbb P(R) = \frac{1}{4}} и Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathbb P(B) = \frac{1}{2}.} Каковы шансы у Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle R} против Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle B} ? Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathbb P(R) : \mathbb P(B) = \left(\frac{1}{4} : \frac{1}{2}\right),} разумеется.
Точно так же, мы можем взять шансы Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \left(\frac{\mathbb P(R)}{\mathbb P(B)} : 1\right)} , потому что Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \frac{\mathbb P(R)}{\mathbb P(B)}} настолько Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle R} вероятней чем Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle B} . В этом примере, Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \frac{\mathbb P(R)}{\mathbb P(B)} = \frac{1}{2},} потому что Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle R} в два раза менее вероятней Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle B} . Иногда, нотация Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \frac{\mathbb P(R)}{\mathbb P(B)}} называется «соотношением шансов Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle R} против Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle B} », что означает шансы Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle R} против Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle B} составляют Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \left(\frac{\mathbb P(R)}{\mathbb P(B)} : 1\right).}
Шансы в соотношения[править]
Когда у нас есть лишь две переменные Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle x} и Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle y} в наборе шансов, шансы могут быть преобразованы в соотношение Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \frac{x}{y}.} Соотношение шансов Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \frac{x}{y}} относится к шансам Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle (x : y),} или эквивалентно к Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \left(\frac{x}{y} : 1\right).}
Статьи по теме[править]
- Оригинал статьи: Odds: Introduction