Водопадные диаграммы и относительные шансы — различия между версиями
Muyyd (обсуждение | вклад) (Новая страница: «Водопадные диаграммы, как и Частотные диаграммы. Первое знакомство с теоремой|частотны…») |
Muyyd (обсуждение | вклад) |
||
| Строка 78: | Строка 78: | ||
Это не значит, что мы, увидев искры, будем думать, что этот виджет плохой. Вероятность стала лишь 25%, что меньше чем 50/50. Но это и не означает, что мы будем думать "Я все еще верю, что этот виджет хороший!", и выкинем свидетельство из головы. Плохой виджет с большей вероятностью будет искрить, следовательно, наблюдая это свидетельство, мы должны ожидать с большей уверенностью, что это виджет плохой, даже если вероятность не поднялась выше 50%. Мы увеличиваем вероятность с 10% до 25%. | Это не значит, что мы, увидев искры, будем думать, что этот виджет плохой. Вероятность стала лишь 25%, что меньше чем 50/50. Но это и не означает, что мы будем думать "Я все еще верю, что этот виджет хороший!", и выкинем свидетельство из головы. Плохой виджет с большей вероятностью будет искрить, следовательно, наблюдая это свидетельство, мы должны ожидать с большей уверенностью, что это виджет плохой, даже если вероятность не поднялась выше 50%. Мы увеличиваем вероятность с 10% до 25%. | ||
}} | }} | ||
| + | |||
| + | Водопады - один из способов визуализировать "шансовую форму" ТБ, которая выражается как: априорные шансы помноженные на условные шансы дают апостериорные шансы. Что в свою очередь можно рассматривать как формализацию концепции "силы свидетельства" или "как сильно мы должны изменить наши убеждения в случае наблюдения свидетельства". В [[Правило Байеса: шансы|следующей статье]] мы рассмотрим более общую форму. | ||
| + | |||
| + | === Статьи по теме === | ||
| + | * [[Теорема Байеса]] | ||
| + | * [[Частотные диаграммы. Первое знакомство с теоремой]] [https://arbital.com/p/bayes_frequency_diagram/?l=55z&pathId=24787 Frequency diagrams: A first look at Bayes ] | ||
| + | * [[Правило Байеса: шансы]] [https://arbital.com/p/bayes_rule_odds/?l=1x8&pathId=24787 Introduction to Bayes' rule: Odds form ] | ||
| + | * [[Условная вероятность]] | ||
| + | * [[Свидетельство]] | ||
Версия 07:17, 27 октября 2017
Водопадные диаграммы, как и частотные, дают возможность визуализировать вывод по ТБ.
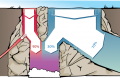
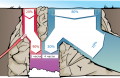
Вообразите водопад с двумя потоками воды на вершине: красным и синим. Они приближаются к вершине раздельно, а потом часть воды в этих потоках уходит в сторону, а часть объединяется в один водоем.
Предположим что:
- С вершины вниз падает 20 литров в секунду красной воды и 80 литров в секунду синей.
- Лишь 90% красной воды попадает в объединенный водоем.
- Лишь 30% синей воды попадает в объединенный водоем.
Сколько всего красной воды и синей воды падает вниз, образуя фиолетовый водоем?
Эта проблема аналогична задаче про Болезнит:
- 20% популяции заражено Болезнитом.
- У 90% зараженных депрессор чернеет.
- У 30% здоровых людей тоже чернеет депрессор.
Эти 20% зараженных аналогичны 20 литрам в секунду красной воды; а 80% здоровых аналогичны 80 литрам в секунду синей воды.
Эти 90% зараженных с почерневшим депрессором аналогичны 90% красной воды, попадающей в фиолетовый водоем. А 30% здоровых пациентов с почерневшим депрессором аналогичны 30% синей воды, попадающей в фиолетовый водоем.
Следовательно, ответ на вопрос "какая часть воды в фиолетовом водоеме из красного потока?" и ответ на вопрос "какая часть пациентов с почерневшим депрессором заражена Болезнитом? совпадают.
А теперь я покажу быстрый способ ответить на тот вопрос из статьи про частотные диаграммы.
На вершине водопада синей воды в 4 раза больше, чем красной.
Потом у каждой молекулы красной воды есть 90% вероятность оказаться в фиолетовом водоеме, а у молекулы синей воды эта вероятность составляет 30%. Так что у молекулы воды шансы в три раза выше (0.90 / 0.30 = 3) оказаться в фиолетовом водоеме.
Мы умножаем априорные пропорции Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 1 : 4 } (соотношение красной и синей воды на вершине) и относительные пропорции Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 3 : 1} и получаем итог Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle (1 \cdot 3) : (4 \cdot 1) = 3 : 4} , что значит - фиолетовый водоем состоит из 3 частей красной воды и четырех частей синей.
Если превратить эти относительные пропорции в абсолютные вероятности того, что случайная молекула воды в фиолетовом водоеме попала туда из красного потока мы вычисляем 3 / (3 + 4)= 3/7, что составляет примерно 47%. Столько воды в фиолетовом водоеме из красного потока.
Эта пропорция точно такая же как и 18 : 24 зараженных с положительным результатом и здоровых с положительным результатом, которую мы получим в ходе решения задачи про 100 пациентов.
Итак, чтобы решить задачу про Болезнит в уме, вам следует превратить эту словесную задачу:
- 20% исследуемой популяции заражены Болезнитом. У 90% зараженных депрессор становится черным, как и у 30% незараженных. С учетом того, что депрессор почернел, какова вероятность того, что у пациента Болезнит?
В такие вычисления:
- Итак, начальные шансы (20% : 80%) = (1 : 4), и относительные шансы (90% : 30%) = (3 : 1). Перемножаем и получаем (3 : 4) что составляет вероятность в 3 / (3 + 4) = 3/7.
(Возможно у вас будут трудности с переводом 3/7 в 43% в уме, но можно прикинуть и будет видно, что вероятность ниже 50%.)
Попробуйте применить этот же способ для такой задачи:
- 90% виджетов плохие, а 10% хорошие.
- 12% плохих виджетов искрят.
- Лишь 4% хороших виджетов искрят.
Какой процент искрящих виджетов состовляют плохие? И если вам понятен метод, попробуйте решить эту задачу в уме.
(Можно даже вообразить виджетопад с плохими и хорошими виджетами на вершине и искрящими виджетами внизу.)
Относительное правдоподобие искрящих плохих виджетов к искрящим хорошим составляет (12 : 4).
Это упрощается в (1 : 9) x (3 : 1) = (3 : 9) = (1 : 3), т.е. на 1 плохой искрящийся виджет приходится 3 хороших искрящихся.
Что превращается в вероятность 1/(1+3) = 1/4 = 25%; т.е. 25% искрящихся виджетов плохие.
Водопады - один из способов визуализировать "шансовую форму" ТБ, которая выражается как: априорные шансы помноженные на условные шансы дают апостериорные шансы. Что в свою очередь можно рассматривать как формализацию концепции "силы свидетельства" или "как сильно мы должны изменить наши убеждения в случае наблюдения свидетельства". В следующей статье мы рассмотрим более общую форму.