Правило Байеса: шансы — различия между версиями
Muyyd (обсуждение | вклад) |
Muyyd (обсуждение | вклад) |
||
| Строка 79: | Строка 79: | ||
[[Априорная вероятность|Априорные]] шансы означают соотношение больных пациентов к здоровым <math>1 : 4</math>. Превращение этих шансов в вероятности даст нам <math>\mathbb P(sick)=\frac{1}{4+1}=\frac{1}{5}=20\%</math>. | [[Априорная вероятность|Априорные]] шансы означают соотношение больных пациентов к здоровым <math>1 : 4</math>. Превращение этих шансов в вероятности даст нам <math>\mathbb P(sick)=\frac{1}{4+1}=\frac{1}{5}=20\%</math>. | ||
| + | |||
| + | The [-relative_likelihood] refers to how much more likely each sick patient is to get a positive test result than each healthy patient, which (using [conditional_probability conditional probability notation]) is $\frac{\mathbb P(positive \mid sick)}{\mathbb P(positive \mid healthy)}=\frac{0.90}{0.30},$ aka relative likelihoods of $3 : 1.$ | ||
| + | |||
| + | [[Соотношение условных шансов|Соотношение условных шансов]] означает соотношение того, насколько вероятней у больного пациента почернеет депрессор к к положительному результату у здорового, что с использованием обозначения для [[Условная вероятность|условных вероятностей]] будет выглядеть как <math>\frac{\mathbb P(positive \mid sick)}{\mathbb P(positive \mid healthy)}=\frac{0.90}{0.30},</math> т.е. соотношение условных шансов будет <math>3 : 1.</math> | ||
| + | |||
| + | [[Апостериорная вероятность|Апостериорные]] шансы означают соотношение больных пациентов к здоровым среди всех с положительным результатом, что выражается как <math>\frac{\mathbb P(sick \mid positive)}{\mathbb P(healthy \mid positive)} = \frac{3}{4}</math>, т.е. шансы <math>3 : 4</math>. | ||
| + | |||
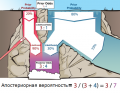
| + | Для извлечения вероятности из шансов нам следует держать в уме, что [[Взаимоисключающие и исчерпывающие гипотезы|полная вероятность взаимоисключающих событий ]] в сумме всегда составляет <math>1,</math> т.е. есть 100% вероятность для ''чего-то''. Раз уж все либо болеют либо здоровы, мы можем [[Нормализация вероятностей|нормализовать]] соотношение шансов <math>3 : 4</math> путем деления их на сумму: <math>(\frac{3}{3+4} : \frac{4}{3+4}) = (\frac{3}{7} : \frac{4}{7}) \approx (0.43 : 0.57)</math> | ||
| + | |||
| + | ...что в итоге дает нам вероятности <math>(0.43 : 0.57)</math>, пропорциональные шансам <math>(3 : 4)</math>, с суммой в <math>1</math>. Будет странно иметь вероятность в <math>3</math> (300%) для какого-то события. | ||
| + | |||
| + | Если визуализировать это с помощью водопадной диаграммы: | ||
| + | |||
| + | <gallery> | ||
| + | 4CXsoZhA.png | ||
| + | </gallery> | ||
| + | |||
| + | Мы можем обобщить это для любых конкурирующих гипотез <math>H_j</math> и <math>H_k</math> и свидетельства <math>e</math>, что теорема Байеса может быть записана как: | ||
| + | |||
| + | <math>\dfrac{\mathbb P(H_j)}{\mathbb P(H_k)} \times \dfrac{\mathbb P(e \mid H_j)}{\mathbb P(e \mid H_k)} = \dfrac{\mathbb P(H_j \mid e)}{\mathbb P(H_k \mid e)}</math> | ||
| + | |||
| + | что говорит нам: "соотношение апостериорных шансов для конкурирующих гипотез <math>H_j</math> и <math>H_k</math> (при условии наблюдения свидетельства <math>e</math>), равно произведению априорных шансов с соотношением того, как <math>H_j</math> предсказывает свидетельство в сравнении с <math>H_k.</math>" | ||
| + | |||
| + | Если <math>H_j</math> и <math>H_k</math> [[Взаимоисключающие и исчерпывающие гипотезы|взаимоисключающие и исчерпывающие]], мы можем конвертировать апостериорные шансы в апостериорную вероятность для <math>H_j</math> путем [[Нормализация вероятностей|нормализации]] шансов: делением соотношения шансов на их сумму, чтобы элементы нового соотношения суммировались к <math>1</math>. | ||
| + | |||
| + | === Доказательство теоремы Байеса === | ||
| + | |||
| + | Rearranging [conditional_probability the definition of conditional probability], $\mathbb P(X \wedge Y) = \mathbb P(Y) \cdot \mathbb P(X|Y).$ E.g. to find "the fraction of all patients that are sick *and* get a positive result", we multiply "the fraction of patients that are sick" times "the probability that a sick patient blackens the tongue depressor". | ||
| + | |||
| + | Перестроим [[Условные вероятности|определение условных вероятностей]] <math>\mathbb P(X \wedge Y) = \mathbb P(Y) \cdot \mathbb P(X|Y).</math> Т.е. чтобы найти "часть всех пациентов которые больны и с положительным результатом" мы перемножаем "часть пациентов, которые больны" и "вероятность того, что у зараженного пациента почернеет депрессор". | ||
| + | |||
| + | Тогда доказательство теоремы Байеса, где <math>e_0</math> - новое свидетельство, будет выглядеть так: | ||
| + | |||
| + | |||
| + | |||
| + | <math> | ||
| + | \frac{\mathbb P(H_j)}{\mathbb P(H_k)} | ||
| + | \cdot | ||
| + | \frac{\mathbb P(e_0 | H_j)}{\mathbb P(e_0 | H_k)} | ||
| + | = | ||
| + | \frac{\mathbb P(e_0 \wedge H_j)}{\mathbb P(e_0 \wedge H_k)} | ||
| + | = | ||
| + | \frac{\mathbb P(H_j \wedge e_0)/\mathbb P(e_0)}{\mathbb P(H_k \wedge e_0)/\mathbb P(e_0)} | ||
| + | = | ||
| + | \frac{\mathbb P(H_j | e_0)}{\mathbb P(H_k | e_0)} | ||
| + | </math> | ||
| + | ч.т.д. | ||
| + | |||
| + | In the Diseasitis example, these proof steps correspond to the operations: | ||
| + | |||
| + | Для задачи про Болезнит, шаги этого доказательства соответствуют операциям: | ||
| + | |||
| + | |||
| + | |||
| + | <math> | ||
| + | \frac{0.20}{0.80} | ||
| + | \cdot | ||
| + | \frac{0.90}{0.30} | ||
| + | = | ||
| + | \frac{0.18}{0.24} | ||
| + | = | ||
| + | \frac{0.18/0.42}{0.24/0.42} | ||
| + | = | ||
| + | \frac{0.43}{0.57} | ||
| + | </math> | ||
| + | |||
| + | Using red for sick, blue for healthy, grey for a mix of sick and healthy patients, and + signs for positive test results, the calculation steps can be visualized as follows: | ||
| + | |||
| + | Используя красный цвет для обозначения больных, синий - для здоровых, серый для смеси больных и здоровых, и знак "+" для положительного результата, можно визуализировать вычисления: | ||
| + | |||
| + | <gallery> | ||
| + | 5YBc2nYo.png | ||
| + | </gallery> | ||
| + | |||
| + | This process of observing evidence and using its likelihood ratio to transform a prior belief into a posterior belief is called a "[bayes_update Bayesian update]" or "belief revision." | ||
| + | |||
| + | Этот процесс, где мы наблюдаем свидетельства и используем соотношение условных вероятностей (отношения правдоподобия) для трансформации априорных убеждений в апостериорные называется "[[Байесианский апдейт| байесианским апдейтом]]" или же "пересмотром убеждений. | ||
| + | |||
| + | === Статьи по теме === | ||
| + | *Каталог статей гайда по ТБ: [[Теорема Байеса]] | ||
| + | *Предыдущая статья в гайде: [[Водопадные диаграммы и относительные шансы]] | ||
| + | *Следующая статья в гайде: [https://arbital.com/p/bayes_extraordinary_claims/?pathId=24787 Extraordinary claims require extraordinary evidence ] | ||
Версия 10:46, 1 ноября 2017
В одной из формулировок байесовское правило выглядит так: априорные шансы х соотношение условных шансов = апостериорные шансы.
Если мы рассмотрим водопадную визуализацию проблемы с Болезнитом, то будет наглядно видно, как относительные шансы помогают думать про два потока на вершине водопада.
Пропорциональное соотношение воды из красного потока к воде из синего будет тем же, независимо от того идет ли речь 200 и 800 литрах в секунду или о 20 000 и 80 000 литрах в секунду илл о 1 и 4 л/с. Пока и остальная часть водопада способствует сохранению пропорции, мы будем получать такую же пропорцию красной и синей воды внизу. Таким образом мы вполне оправданно можем игнорировать количество воды и рассматривать лишь пропорции.
Точно так же, важно пропорциональное соотношение между количеством попадающей в фиолетовый водоем воды из красного потока к количеству из синего, и соотношение между количеством молекул из каждого литра. Вниз падает 45% и 15% красной и синей воды и точно такое же соотношение между красной и синей водой внизу - 90% и 30%.
И это оправдывает игнорирование специфической информации о том что 90% красной воды падает вниз и 30% синей падает вниз, ведь это можно легко заменить соотношением (3 : 1).
Это можно применить и для других проблем: предположим, что у нас есть медицинский тест, выявляющий болезнь с истинноположительной точностью в 90% (10% ложноотрицательных) и 30% ложноположительных (70% ложноотрицательных). Положительный результат такого теста будет свидетельством такой же силы, как и для теста с 60% истинноположительными и 20% ложноположительными. А отрицательный результат такого теста будет свидетельством такой же силы, как и для теста с 9% ложноотрицательных и 63% истинноотрицательных.
В целом, сила свидетельства является соотношением того, насколько более/менее вероятными разные возможные состояния мира делают наблюдению специфических феноменов. Но об этом позже.
Содержание
Уравнение
Чтобы действительно выразить ТБ в формулах и доказать ее, нам потребуется ввести несколько новых обозначений.
Условная вероятность
Во-первых, если Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle X} это утверждение, то Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P(X)} это вероятность Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle X.}
Другими словами: Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle X} это что-то истинное или ложное в действительности, но у нас есть какая-то неопределенность по этому поводу, и Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle P(X)} - это способ выразить уровень нашей убежденности в том, что Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle X} истинно. Пациент, на самом деле, либо болен либо здоров, но если вы не уверены, свидетельство может способствовать сдвигу субъективной вероятности к 43% в пользу того, что он болен.
Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathbb \neg X} означает "Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle X} ложно", так что Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathbb P(\neg X)} означает "вероятность, что Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle X} ложно".
Задача про Болезнит включала больше утверждений посложней, например:
- Вероятность в 90%, что у пациента почернеет депрессор, при условии что он заражен.
- Вероятность в 30%, что у пациента почернеет депрессор, при условии что он здоров.
- Вероятность в 3/7, что пациент заражен, при условии, что его депрессор почернел.
В этих случаях мы идем от факта про который мы "знаем" или "предполагаем", что он истинен (справа), к утверждению (слева), вероятность которого мы оцениваем, принимая во внимание "известный" факт.
Такие вероятностные утверждения называются "условными вероятностями". Если выразить приведенные выше утверждения с помощью стандартных формул, то они будут выглядеть так:
- Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathbb P(blackened \mid sick) = 0.9}
- Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathbb P(blackened \mid \neg sick) = 0.3}
- Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathbb P(sick \mid blackened) = 3/7}
(прим. blackened - почерневший депрессор; sick - зараженный)
<sarcasm>Стандартная запись Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathbb P(X \mid Y)} означающая "вероятность Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle X} , при условии что Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle Y} истинно", содержит "полезную" вертикальную линию, которая, в свою очередь, не дает никаких визуальных подсказок о том, что справа находится предполагаемый факт, а слева - выводимый. </sarcasm>
Вот как определяется условная вероятность, при использовании обозначений Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle X \wedge Y} для обозначения "X и Y" или же "оба Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle X} и Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle Y} истинны":
Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathbb P(X \mid Y) := \frac{\mathbb P(X \wedge Y)}{\mathbb P(Y)}}
Т.е. с точки зрения задачи с Болезнитом, Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathbb P(sick \mid blackened)} вычисляется путем деления 18% больных студентов с почерневшим депрессором (Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathbb P(sick \wedge blackened)} ) на 42% всех с почерневшим депрессором (Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathbb P(blackened)} ).
Или рассмотрим Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathbb P(blackened \mid \neg sick),} - вероятность того, что депрессор почернеет, при условии что пациент здоров. Что эквивалентно делению 24 здоровых студентов с почерневшим депрессором на 80 здоровых. 24 / 80 = 3/10, что соответствует 30% ложноположительных результатов из начальных условий.
Закон условных вероятностей можно выразить так: "Сосредоточим все внимание на возможных мирах, где Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle Y} истинно, или истинны Y-подобные штуки. Рассматривая лишь случаи где Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle Y} истинно, сколько мы найдем случаев внутри этого множества, где еще и Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle X} истинно? Т.е. где истинно Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle Y} и Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle X} ?
Для получения дополнительной информации обратитесь к статье про условные вероятности.
Правило Байеса.
Правило Байеса гласит: априорные шансы х соотношение условных шансов = апостериорные шансы.
Что для задачи про Болезнит будет выглядеть так:
Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \dfrac{\mathbb P({sick})}{\mathbb P(healthy)} \times \dfrac{\mathbb P({blackened}\mid {sick})}{\mathbb P({blackened}\mid healthy)} = \dfrac{\mathbb P({sick}\mid {blackened})}{\mathbb P(healthy\mid {blackened})}.} (прим. blackened - почерневший депрессор; sick - зараженный; healthy - здоровый)
Априорные шансы означают соотношение больных пациентов к здоровым Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 1 : 4} . Превращение этих шансов в вероятности даст нам Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathbb P(sick)=\frac{1}{4+1}=\frac{1}{5}=20\%} .
The [-relative_likelihood] refers to how much more likely each sick patient is to get a positive test result than each healthy patient, which (using [conditional_probability conditional probability notation]) is $\frac{\mathbb P(positive \mid sick)}{\mathbb P(positive \mid healthy)}=\frac{0.90}{0.30},$ aka relative likelihoods of $3 : 1.$
Соотношение условных шансов означает соотношение того, насколько вероятней у больного пациента почернеет депрессор к к положительному результату у здорового, что с использованием обозначения для условных вероятностей будет выглядеть как Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \frac{\mathbb P(positive \mid sick)}{\mathbb P(positive \mid healthy)}=\frac{0.90}{0.30},} т.е. соотношение условных шансов будет Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 3 : 1.}
Апостериорные шансы означают соотношение больных пациентов к здоровым среди всех с положительным результатом, что выражается как Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \frac{\mathbb P(sick \mid positive)}{\mathbb P(healthy \mid positive)} = \frac{3}{4}} , т.е. шансы Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 3 : 4} .
Для извлечения вероятности из шансов нам следует держать в уме, что полная вероятность взаимоисключающих событий в сумме всегда составляет Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 1,} т.е. есть 100% вероятность для чего-то. Раз уж все либо болеют либо здоровы, мы можем нормализовать соотношение шансов Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 3 : 4} путем деления их на сумму: Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle (\frac{3}{3+4} : \frac{4}{3+4}) = (\frac{3}{7} : \frac{4}{7}) \approx (0.43 : 0.57)}
...что в итоге дает нам вероятности Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle (0.43 : 0.57)} , пропорциональные шансам Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle (3 : 4)} , с суммой в Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 1} . Будет странно иметь вероятность в Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 3} (300%) для какого-то события.
Если визуализировать это с помощью водопадной диаграммы:
Мы можем обобщить это для любых конкурирующих гипотез Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle H_j} и Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle H_k} и свидетельства Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle e} , что теорема Байеса может быть записана как:
Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \dfrac{\mathbb P(H_j)}{\mathbb P(H_k)} \times \dfrac{\mathbb P(e \mid H_j)}{\mathbb P(e \mid H_k)} = \dfrac{\mathbb P(H_j \mid e)}{\mathbb P(H_k \mid e)}}
что говорит нам: "соотношение апостериорных шансов для конкурирующих гипотез Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle H_j} и Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle H_k} (при условии наблюдения свидетельства Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle e} ), равно произведению априорных шансов с соотношением того, как Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle H_j} предсказывает свидетельство в сравнении с Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle H_k.} "
Если Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle H_j} и Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle H_k} взаимоисключающие и исчерпывающие, мы можем конвертировать апостериорные шансы в апостериорную вероятность для Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle H_j} путем нормализации шансов: делением соотношения шансов на их сумму, чтобы элементы нового соотношения суммировались к Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle 1} .
Доказательство теоремы Байеса
Rearranging [conditional_probability the definition of conditional probability], $\mathbb P(X \wedge Y) = \mathbb P(Y) \cdot \mathbb P(X|Y).$ E.g. to find "the fraction of all patients that are sick *and* get a positive result", we multiply "the fraction of patients that are sick" times "the probability that a sick patient blackens the tongue depressor".
Перестроим определение условных вероятностей Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \mathbb P(X \wedge Y) = \mathbb P(Y) \cdot \mathbb P(X|Y).} Т.е. чтобы найти "часть всех пациентов которые больны и с положительным результатом" мы перемножаем "часть пациентов, которые больны" и "вероятность того, что у зараженного пациента почернеет депрессор".
Тогда доказательство теоремы Байеса, где Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle e_0} - новое свидетельство, будет выглядеть так:
Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \frac{\mathbb P(H_j)}{\mathbb P(H_k)} \cdot \frac{\mathbb P(e_0 | H_j)}{\mathbb P(e_0 | H_k)} = \frac{\mathbb P(e_0 \wedge H_j)}{\mathbb P(e_0 \wedge H_k)} = \frac{\mathbb P(H_j \wedge e_0)/\mathbb P(e_0)}{\mathbb P(H_k \wedge e_0)/\mathbb P(e_0)} = \frac{\mathbb P(H_j | e_0)}{\mathbb P(H_k | e_0)} } ч.т.д.
In the Diseasitis example, these proof steps correspond to the operations:
Для задачи про Болезнит, шаги этого доказательства соответствуют операциям:
Невозможно разобрать выражение (MathML с переходом в SVG или PNG (рекомендуется для современных браузеров и инструментов повышения доступности): Недопустимый ответ («Math extension cannot connect to Restbase.») от сервера «https://en.wikipedia.org/api/rest_v1/»:): {\displaystyle \frac{0.20}{0.80} \cdot \frac{0.90}{0.30} = \frac{0.18}{0.24} = \frac{0.18/0.42}{0.24/0.42} = \frac{0.43}{0.57} }
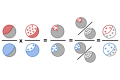
Using red for sick, blue for healthy, grey for a mix of sick and healthy patients, and + signs for positive test results, the calculation steps can be visualized as follows:
Используя красный цвет для обозначения больных, синий - для здоровых, серый для смеси больных и здоровых, и знак "+" для положительного результата, можно визуализировать вычисления:
This process of observing evidence and using its likelihood ratio to transform a prior belief into a posterior belief is called a "[bayes_update Bayesian update]" or "belief revision."
Этот процесс, где мы наблюдаем свидетельства и используем соотношение условных вероятностей (отношения правдоподобия) для трансформации априорных убеждений в апостериорные называется " байесианским апдейтом" или же "пересмотром убеждений.
Статьи по теме
- Каталог статей гайда по ТБ: Теорема Байеса
- Предыдущая статья в гайде: Водопадные диаграммы и относительные шансы
- Следующая статья в гайде: Extraordinary claims require extraordinary evidence