Вы здесь
Главные вкладки
Нормальные распределения в предсказаниях
Предсказания - хорошая практика, особенно, если их записывать.
Однако мы часто делаем бинарные предсказания тогда, когда это вовсе не требуется:
- Байден победит на всенародном голосовании: 91%
- Число смертей от COVID в Дании перевалит за 10000 до конца года: 84%
Вместо этого мы можем делать предсказания, используя нормальные распределения:
- Доля голосов за Байдена на всенародном голосовании ~ N(0.54, 0.03)
- Число смертей от COVID в Дании до конца года ~ N(15000, 5000)
(„~“ означает „имеет распределение“)
Составление «нормальных» предсказаний может показаться запутанным, но этого эссе должно быть достаточно, чтобы понять основы и, самое главное, научиться отслеживать свою калибровку, что гораздо сложнее делать с бинарными предсказаниями.
Ключевые моменты:
1. Предсказывать по нормальным распределениям на удивление просто.
2. Для получения числа, показывающего насколько сильно вы пере/недо оцениваете свою уверенность, достаточно простой математики!
3. Нормальное распределение содержит больше информации, чем Бернулли (бинарный результат, как при бросании монетки) и, как следствие, позволяет сделать более точные выводы!
Вопросы, на которые ответит это эссе:
1. Как мне сделать «нормальное» предсказание?
2. Зачем мне это?
3. Как мне отслеживать свою калибровку?
Коротко о нормальном распределении
Нормальное распределение обычно записывается как N($\mu$,$\sigma$) и имеет 2 параметра:
- среднее значение $\mu$ (произносится «мю»), которое является одновременно и медианой, и модой, и матожиданием
- среднеквадратическое отклонение $\sigma$ (произносится «сигма»), которое показывает неуверенность
Правило трёх сигм гласит:
- 68% ваших предсказаний должны попадать в интервал $\mu\pm1\sigma$
- 95% ваших предсказаний должны попадать в интервал $\mu\pm2\sigma$
- 99.7% ваших предсказаний должны попадать в интервал $\mu\pm3\sigma$
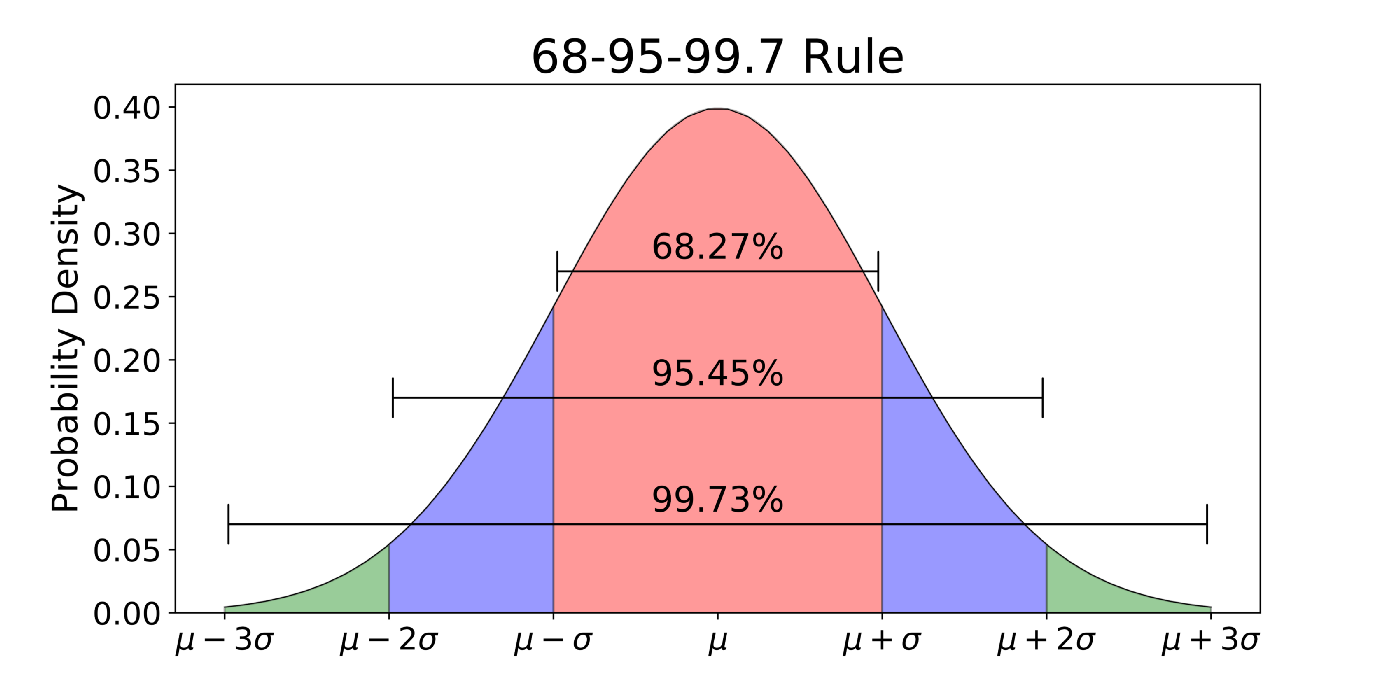
50% предсказаний должны оказаться в пределах $0.674\sigma\approx\frac{2}{3}\sigma$ от среднего значения, это число можно использовать для быстрой проверки
Последняя мелочь, которую нам нужно помнить: дисперсия нормального распределения это просто $\sigma^2$:
$$
Var(N(\mu, \sigma)) = \sigma^2
$$
Как делать предсказания
Предсказание состоит из двух шагов: предсказание $\mu$ и использование правила трёх сигм, чтобы подобрать вашу неуверенность в $\mu$.
Я попытался спрогнозировать долю голосов за Байдена на выборах 2020 года. По результатам опросов я получил точечную оценку 54%, это $\mu$. Используем правило трёх сигм и посмотрим, что это будет означать для различных значений $\sigma$. Таблица для $\sigma$ от 2 до 5:

$\sigma=2$ подразумевает шанс 97.5% (интервал 95% + половина остатка), что Байден получит более 50% голосов; я не был настолько уверен. $\sigma=4$ подразумевает шанс 84% (68% + 32%/2), что Байден получит более 50% голосов, и шанс 16% победы Трампа. Это я посчитал слишком высоким, поэтому остановился на $\sigma=3$.
Зачем это нужно
Байден получил 52% голосов, что было в пределах одной сигма от моего предсказания. Таким образом, я извлёк два слабых урока из ОДНОЙ точки данных:
1. Организаторы опросов облажались, так что мне следовало сместить $\mu$ в сторону среднего значения (50%), предсказав, например, 53% вместо 54%.
2. Реальное значение было ровно в $\frac{2}{3}\sigma$ от $\mu$, так что $\sigma$ оказалась на 50%/50% границе, как и ожидалось. Мне повезло, но это слабое свидетельство, что $\sigma$ была подобрана хорошо.
Представьте, что вместо этого я предсказал что Байден победит (на всенародном голосовании) с вероятностью 91%. Ну, он победил, так что я был прав… и на этом всё. Странно думать, что мне стоило предсказать 80%, так как организаторы опросов облажались, ведь это более слабое предсказание, а более сильное оказалось верным! Мне бы потребовалось предсказать результаты множества других выборов, чтобы заметить, что моя уверенность слишком низка или высока.
Как отслеживать свою калибровку
Замечание: В прошлом разделе мы использовали для предсказаний $\mu$ и $\sigma$. В этом разделе мы будем использовать $\mu_i$ и $\sigma_i$, где i это индекс (предсказание 1, предсказание 2… предсказание N). Мы воспользуемся $\hat{\sigma}_z$ для оценки точки калибровки; то есть $\hat{\sigma}_z$ это число, такое как 1.73. В следующем эссе в серии, мы будем использовать $\sigma_z$ для калибровочного распределения.
Я также сделал ужасное предсказание во время ранних дней локдауна в 2020. Я предсказал N(15000, 5000) смертей от COVID в Дании до начала 2022 года. Наблюдаемое значение составило 3 200, что находится на расстоянии $\frac{15000 - 3200}{5000}=2.36$ стандартных отклонений от моего предсказания, то есть за пределами 95% интервала!
В этом разделе мы приведём наши предсказания к общему виду, который называется стандартизированной или z-оценкой. Если все наши предсказания находятся на одной стандартной шкале, мы можем их сравнивать.
$$
z_{ideal} \sim N(0, 1) \
Var(z_{ideal}) = 1^2=1
$$
Обычно когда мы преобразуем к z-оценкам, мы используем саму информацию, чтобы рассчитать $\mu$ и $\sigma$, что гарантирует распределение N(0, 1). Сейчас мы воспользуемся нашими предсказанными $\mu$ и $\sigma$. Это означает, что между $z_{идеальное}$ и нашим $z$ будет расхождение. Это расхождение показывает, насколько мы недо/пере оцениваем предсказанные интервалы, а следовательно описывает нашу калибровку. То есть, например, если $\hat{\sigma_z} = 2$, то все наши интервалы должны быть в два раза шире, чтобы достигнуть $z_{перекалиброванное} \sim N(0, 1)$.
Сначала мы производим z-оценку наших предсказаний, рассчитывая, на сколько $\sigma$ они отличаются от наблюдаемых значений $x$ по этой формуле:
$$
z_i = \frac{\mu_i - x_i}{\sigma_i}
$$
Затем мы рассчитываем $\hat{\sigma}_z$ - среднее квадратичное отклонение от всех предсказаний:
$$
Var(z) = \sum_{i=0}^N Var(z_i) = \sum_{i=0}^N z_i^2
$$
$$
\hat{\sigma}_z = \sqrt{\frac{Var(z)}{N}}
$$
Давайте посчитаем $\hat{\sigma}_z$ для моих двух предсказаний. Сначала дисперсии:
- $Var(z_1)=(\frac{54-52}{3})^2=\frac{4}{9}$
- $Var(z_2)=(\frac{15000 - 3200}{5000})^2=5.57$
Затем считаем $\hat{\sigma}_z$:
$$
\hat{\sigma}_z = \sqrt{\frac{Var(z)}{N}} = \sqrt{\frac{\frac{4}{9} + 5.57}{2}} = 1.73
$$
Так что если учитывать только эти два моих предсказания, я должен расширить свой интервал на 73%. Другими словами, так как $\hat{\sigma}_z$ равна 1.73, а не 1, мои интервалы в 1.73 раза уже, чем должны быть. Если бы я получил $\hat{\sigma}_z<1$, например $\hat{\sigma}_z=0.5$, это было бы свидетельством того, что мои интервалы чересчур широки и должны быть сужены, путём умножения на 0.5.
Всё ещё не убеждены?
Вот несколько бонусных аргументов:
1. Слабые 50/50: Иногда мы действительно уверены в чём-то на 50%, как пример рассмотрим предсказание Скотта Александра о том, достигнет ли курс Биткоина 3000 в 2019; эти бинарные 50%/50% могут быть переформулированны как "Биткоин ~ N(3000, 1500)" так что цена в 10000 засчитывается против предсказания. Теперь даже слабые предсказания генерируют свидетельства для калибровки!
2. Завышение и занижение: Если бы Байден получил 20 или 80% голосов, оба исхода были бы сильными свидетельствами того, что моё предсказание неверно, тогда как бинарное предсказание может указать на ошибку в одном направлении.
3. Предсказания с высокой уверенностью проще калибровать: В бинарной стране предсказания с уверенностью 99% очень сложно откалибровать, потому что нам нужно сделать сотни таких предсказаний чтобы собрать достаточно информации (если, конечно, многие из них не окажутся ложными сразу). Соответствующее нормальное предсказание будет иметь маленькую $\sigma$ и, соответственно, давать нам столько же свидетельств для калибровки, как и 60% предсказание.
4. Правота по ошибке: N(50.67, 0.5), N(54, 3), N(58, 6) - все эти распределения дают Байдену 91% шанс на победу, но по совершенно разным причинам, каждое из них приведёт к разным изменениям калибровки после наблюдения $x=52$.
Продвинутые техники
Иногда ваши убеждения не следуют нормальному распределению. Например, предсказание курса Биткоина N(3000, 1500) подразумевает наличие шанса 2.5%, что цена станет негативной, что невозможно. Вот три решения этой проблемы в порядке возрастания навороченности:
- Своя $\sigma$ для каждого направления::
$$
Bitcoin \sim 0.5 HN(3000, \sigma_{up}=3000) + 0.5 HN(3000, \sigma_{down}=1500)
$$
(HN = Half Normal)
То есть если курс выше 3000, то $\sigma=3000$, а если курс ниже, то $\sigma=1500$. Если мы следуем этой схеме, то при калибровке можно использовать соответствующую сигму и игнорировать другую. Так что если курс Биткоина окажется $x=10.000$, то z станет $\frac{7}{3}$:
$$
z = \frac{3000 - 10000}{3000}=-\frac{7}{3}
$$
- Часто мы считаем, что что-то увеличивается или уменьшается в разы, как, например, удваивающийся или падающий в два раза Биткоин. Представим, что Скотт подумал, что курс Биткоина изменится менее чем в два раза с шансом 68%.
$$
\mu = log_{10}(3000) \approx 3.477 \
\sigma = log_{10}(2) \approx 0.301 \
log_{10}(Bitcoin) \sim N( 3.477, 0.301)
$$
z-оценка работает точно так же, то есть если курс Биткоина составил 10000:
$$
log_{10}(x) = log_{10}(10.000) = 4 \
z \approx \frac{3.477 - 4}{0.301} \approx -1.74
$$
- (Если эта часть непонятна, просто пропустите): Можно использовать и произвольное распределение, в этом случае сконвертируйте его в $U(0, 1)$ с помощью функции распределения, а затем преобразуйте к z-оценке, используя обратную к функции распределения. Полученную z-оценку можно использовать при калибровке.
Заключительные замечания
Давайте остановимся, чтобы оценить тот факт, что мы смогли получить конкретное значащее число после двух предсказаний, что практически невозможно при бинарных предсказаниях!
В заключение, имейте эти отличия в виду:
1. Если результат $x$ и предсказание $\mu$ близки, значит вы хороший предсказатель.
2. Если средняя ошибка предсказаний на z-шкале близка к 1, значит вы хорошо откалиброванный предсказатель.
Чтобы преуспевать в первом, необходимы обширные знания, относящиеся к каждому конкретному предсказанию, тогда как калибровка это общий навык, который относится сразу ко всем предсказаниям.
В этом эссе мы рассчитали точечную оценку $\hat{\sigma}_z=1.73$ на основании двух точек данных. В подобных оценках присутствует большая неточность, так что нам следует ожидать, что распределение калибровки вокруг $\sigma_z$ будет весьма широким. В следующем эссе мы разберёмся с этим, путём расчёта самого частого доверительного интервала для $\hat{\sigma}_z$ и Байесовской апостериорной вероятности для $\sigma_z$. Это позволит нам делать такие заявления, как: Я на 90% уверен, что $1<\sigma_z$, а значит, я скорее плохо откалиброван, чем неудачлив. Впрочем, по двум точкам сложно найти разницу с высокой степенью уверенности.
И, наконец, я хотел бы выразить признательность моим редакторам, Justis Mills and eric135, за то что сделали этот текст читабельным.
- Короткая ссылка сюда: lesswrong.ru/1043