ЧаВо по теории принятия решений

1. Что такое «теория принятия решений?

Теория принятия решений, также известная как теория рационального выбора – это наука о предпочтениях, неуверенности и других понятия, связанных с совершением «оптимального» или «рационального» выбора. Ею занимаются экономисты, психологи, философы, математики, статистики и информатики.

Мы можем разделить теорию принятия решений на три части (Грант и Зандт, 2009; Бэрон, 2008). Нормативная теория принятия решений изучает, как бы выбирал идеальный агент (идеально-рациональный, с бесконечной вычислительной мощностью, и т.д.). Дескриптивная теория принятия решений изучает, как на самом деле совершают выбор неидеальные агенты (например, люди). Прескриптивная теория принятия решений изучает, как неидеальные агенты могут усовершенствовать свой процесс принятия решений (относительно нормативной модели), несмотря на свою неидеальность.

Например, одна из нормативных моделей – теория ожидаемой полезности, которая заявляет, что рациональный агент выбирает действия с наивысшей ожидаемой полезностью. Неоднократно воспроизведённые результаты из психологии описывают, как у людей не получается максимизировать ожидаемую полезность, в частности, предсказуемым образом. Например, они могут совершать некоторые выборы, основываясь не на потенциальной будущей выгоде, а на уже не относящихся к делу прошлых усилиях («ошибка невозвратных затрат»). Чтобы помочь людям избегать этой ошибки, некоторые теоретики рекомендуют некоторое базовое обучение микроэкономике. Было показано, что оно снижает склонность совершать эту ошибку (Лэррик и пр. (1990)). Таким образом, координация нормативных, дескриптивных и прескриптивных исследований может помочь агентам преуспевать, в большей степени соответствуя нормативной модели, чем они бы соответствовали самостоятельно.

Это ЧаВо сосредоточено на нормативной теории принятия решений. Некоторые хорошие источники по дескриптивной и прескриптивной: Стэнович (2010) и Хэсти и Доус (2009).

Две близких области, которые всё же выходят за пределы темы этого ЧаВо, это теория игр и теория социального выбора. Теория игр – это изучение конфликта и кооперации многих принимающих решения агентов, так что её иногда называют «интерактивной теорией принятия решений». Теория социального выбора изучает принятие коллективных решений при помощи разных способов комбинирования предпочтений многих агентов.

Этот ЧаВо сильно заимствует из двух учебников по теории принятия решений: Резник (1987) и Петерсон (2009). Ещё он использует некоторые более новые результаты, опубликованные в журналах вроде Synthese и Theory and Decision.

2. Всегда ли рациональное решение – правильное?

Нет. Петерсон (2009, гл. 1) объясняет:

[В 1700 году], Король Швеции Карл и его восьмитысячная армия атаковала русскую армию, численность которой была примерно в десять раз больше… Большинство историков сходятся на том, что атака шведов была иррациональна, почти обречена на провал… Но из-за неожиданной метели, ослепившей русскую армию, шведы победили…

Задним числом можно сказать, что решение шведов атаковать русскую армию было, несомненно, правильным, потому что настоящим результатом оказалась победа. Но, так как у шведов не было хорошего повода ожидать, что они победят, решение, всё же, было иррациональным.

Говоря более обобщённо, мы можем сказать, что решение правильное тогда и только тогда, когда его настоящий результат как минимум настолько же хорош, как у любого другого возможного исхода. А что решение рациональное мы говорим тогда и только тогда, когда тот, кто принимает решение [_или_ «агент»] выбирает то, для чего имеет самые хорошие причины в тот момент, когда решение принимается.

К сожалению, мы не можем точно знать, какое решение правильное. Так что, лучшее, что нам доступно – пытаться принимать «рациональные» или «оптимальные» решения на основе своих предпочтений и неполной информации.

3. Как лучше понять задачу принятия решений?

Для начала, нам надо формализовать задачу. Обычно помогает её ещё и визуализировать.

В теории принятия решений правила применимы только для формализованной задачи. А формализацию можно по-разному визуализировать. Вот пример из Петерсона (2009, гл. 2):

Пусть… вы думаете о том, страховать ли свой дом от пожара. Пусть страховка дома, который стоит \$100,000 стоит \$100. Вы задаётесь вопросом: стоит ли оно того?

Типичный способ формализовать задачу принятия решений: разбить её на состояния, действия и исходы. Столкнувшись с задачей, тот, кто принимает решения, стремиться выбрать действие у которого будет наилучший исход. Но исход каждого действия зависит от состояния мира, которое принимающему не известно.

В этом подходе, грубо говоря, состояние – это та часть мира, которая не действие (которое может быть исполнено сейчас тем, кто принимает решение) и не исход (вопрос о том, что означает состояние более точно сложен, и в этом документе мы его рассматривать не будем). К счастью, не все состояния важны для каждой конкретной задачи. Нам надо принимать во внимание только те состояния, которые затрагивают предпочтения агента касательно действий. Простая формализация задачи о страховке может включать только два состояния: одно, в котором в вашем доме (потом) не будет пожара, и другое, в котором в вашем доме (потом) будет пожар.

Предположительно, агент предпочитает некоторые исходы другим. Скажем, что в нашей задаче есть четыре исхода: (1) Дом и \$0, (2) Дом и -\$100, (3) Нет дома и \$99,900, и (4) Нет дома и \$0. В таком случае, принимающий решения может предпочитать исход 1 исходу 2, исход 2 исходу 3, а исход 3 – исходу 4. (Мы обсудим меру ценности исходов в следующем разделе.)

Действие обычно считается функцией, которая принимает возможное состояние мира и выдаёт конкретный исход. Если в нашей задаче действие «Страховать» получило на вход состояние мира «Пожар», то оно выдаёт исход «Нет дома и \$99,900» на выход.

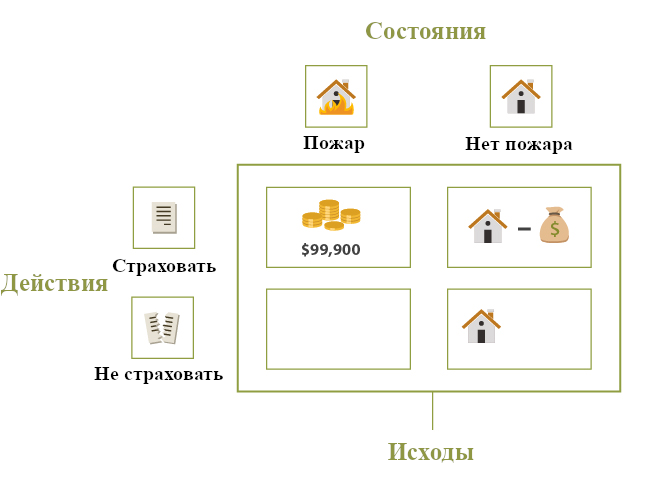
Диаграмма с состояниями, действиями и исходами в нашем примере с страховкой

Заметим, что теория принятия решений интересуется конкретными действиями, а не действиями вообще, т.е. «плыть на запад в 1492», а не «плыть». Более того, действия в задаче принятия решений должны быть альтернативами – то есть, тот, кто принимает решение, должен выбрать ровно одно из них.

Когда задача принятия решений формализована, её затем можно визуализировать. Есть несколько способов.

Один из них – использовать матрицу принятия решений:

	Пожар	Нет пожара
Страховать	Нет дома и \$99,900	Дом и -\$100
Не страховать	Нет дома и \$0	Дом и \$0

Другая визуализация: использовать дерево принятия решений:

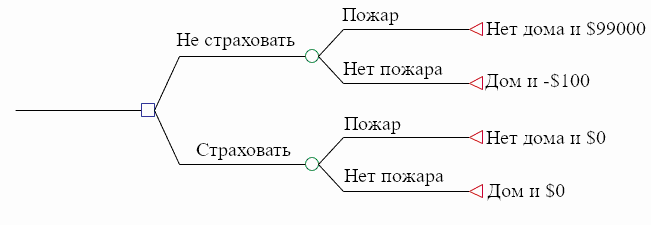
Квадрат – вершины выбора, круги – вершины шанса, а треугольники – конечные вершины. В вершине выбора принимающий решение выбирает, в какую часть дерева отправиться. В вершинах шансов природа выбирает, в какую часть дерева отправиться. Треугольники соответствуют исходам.

Конечно, мы можем добавлять больше веток вершинам выбора и вершинам шансов. Ещё можно использовать больше вершин выбора, тогда мы изобразим задачу последовательных выборов. Наконец, мы можем добавить каждой ветви вероятности, главное, чтобы вероятности ветвей, исходящих из одного узла суммировались в единицу. И, так как дерево принятия решений подчиняется законам теории вероятности, мы можем вычислить вероятность каждого узла, перемножив вероятности всех ветвей на пути к нему.

Ещё наша задача принятия решений может быть представлена как вектор – упорядоченный список математических объектов. Пожалуй, это самый удобный вариант для компьютеров:

[
[a1 = страховать,
a2 = не страховать];
[s1 = пожар,
s2 = нет пожара];
[(a1, s1) = Нет дома и \$99,900,
(a1, s2) = Дом и -\$100,
(a2, s1) = Нет дома и \$0,
(a2, s2) = Дом и \$0]
]

Более подробно о формализации и визуализации задач принятия решений можно прочитать в Скиннер (1993).

4. Как можно измерить предпочтения агента?

4.1. Понятие полезности

Важно не измерять предпочтения агента через объективные меры, например, денежные стоимости. Чтобы увидеть, почему, рассмотрим нелепицы, которые могут получиться, если мы будем измерять предпочтения агента деньгами.

Предположим, вы можете выбрать между (A) точно получить миллион долларов, и (B) 50% получить три миллиона, а 50% – ничего. ожидаемая денежная ценность (ОДЦ) вашего действия вычисляется перемножением денежной ценности каждого исхода на его вероятность. Так что ОДЦ варианта A будет (1)(\$1 млн.) = \$1 млн. ОДЦ варианта B будет (0.5)(\$3 млн.) + (0.5)($0) = \$1.5 млн. ОДЦ варианта B выше, но многие люди предпочли бы гарантированный миллион.

Почему? Для многих людей субъективная разница между \$0 и \$1 млн. намного выше, чем между \$1 млн. и \$3 млн., хоть вторая разница больше в долларах.

Чтобы говорить о субъективных предпочтениях агента мы используем понятие полезности. Функция полезности так присваивает числа исходам, чтобы исходы с более высокими значениями были предпочтительнее исходов с менее высокими. Например, для конкретного принимающего решение – скажем, того, у которого совсем нет денег – полезность \$0 может быть 0, полезность \$1 млн. может быть 1000, а полезность \$3 млн. может быть 1500. Тогда ожидаемая полезность (ОП) варианта A для этого принимающего решение будет равна (1)(1000) = 1000. А ОП варианта EU будет равна (0.5)(1500) + (0.5)(0) = 750. Так что получается, что у варианта A выше ожидаемая полезность, несмотря на то, что у варианта B больше ожидаемая денежная ценность.

Замечу, что люди, которые занимаются статистикой, говоря о теории принятия решений, часто упоминают «функцию потерь». Это попросту величина, обратная функции полезности. Обзор теории принятия решений с этой точки зрения можно прочитать у Бергера (1985) и у Роберта (2001), а критику некоторых стандартных результатов статистической теории принятия решений – в Джейнса (2003, гл. 13).

4.2. Разновидности полезности

Функцию полезности агента нельзя наблюдать напрямую, так что надо её конструировать – например, спрашивая, какие варианты предпочтительнее, о большом наборе пар альтернатив (примерно как на WhoIsHotter). Число, которое соответствует полезности исхода, может значить разные вещи, в зависимости от используемой шкалы полезности. Та же зависит от процедуры конструирования функции полезности.

В теории принятия решений различают три вида шкал полезности:

1. Ординальная шкала («12 – лучше чем 6»). На ординальной шкале предпочитаемым исходам соответствуют более высокие числа, но числа ничего не говорят нам о разницах или соотношениях полезностей разных исходов.
2. Интервальная шкала («разница между 12 и 6 равна разнице между 6 и 0»). Интервальная шкала даёт нам больше информации, чем ординальная. Предпочитаемым исходам тоже присваиваются более выские числа, но тут числа ещё и отображают разницу между полезностями разных исходов. Однако, они могут и не отображать их соотношения. Если на интервальной шкале у исхода A полезность 0, у исхода B – 6, а у исхода C – 12, то мы знаем, что разница полезности между исходами A и B равна разнице полезности между исходами B и C, но не знаем, можно ли сказать, что исход B «вдвое лучше» исхода A.
3. Пропорциональная шкала («12 в точности вдвое ценнее, чем 6»). Числа полезности на пропорциональной шкале дают нам больше всего информации. Они отображают порядок, разницы и соотношения предпочтений. В таком случае можно сказать, что исход с полезностью 12 в точности вдвое ценнее для данного агента, чем исход с полезностью 6.

Заметим, что ни переживаемая полезность (счастье), ни понятия «средней полезности» или «общей полезности», которые рассматривают утилитаристские философы морали, не то же самое, что полезность выбора, которую мы тут используем для описаний предпочтений при решениях. В конкретной ситуации мы можем уточнять дополнительно. Например, описывая функцию полезности выбора на интервальной шкале, сконструированную при помощи аксиоматического подхода Фон Нейнана – Моргенштерна (см. раздел 8), иногда используют термин VNM-полезность.

Теперь вы знаете, что предпочтения агента могут быть представлены как «функция полезности», и что присвоение полезности исходам может иметь разный смысл в зависимости от шкалы полезности, мы можем более формально думать о задаче совершения «оптимальных» или «рациональных» выборов. (Мы ещё вернёмся к задаче конструирования функции полезности агента в разделе 8.3)

5. Что в теории принятия решений имеют в виду под «риском», «неизвестностью» («ignorance») и «неуверенностью»?

Петерсон (2009, гл. 1) объясняет:

В теории принятия решений повседневные слова вроде риска, неизвестности и неуверенности используются как точные термины с конкретным смыслом. Решение в условиях риска – это решение, при котором совершающий его знает вероятности возможных исходов, а в случае решения в условиях неизвестности вероятности либо неизвестны, либо вообще не определены. Неуверенность используют либо как синоним неизвестности, либо как общий термин для и риска и неизвестности.

В этом ЧаВо мы будем называть «решениями в условиях неизвестности» те, у которых нет присвоенных всем исходам вероятностей, а «решениями в условиях неуверенности» – те, у которых они есть. Слово «риск» мы зарезервируем для обсуждения полезности.

6. Как следует принимать решения в условиях неизвестности?

«Решение в условиях неизвестности» означает, что принимающий решение (1) знает, какие действия можно выбрать, и к каким исходам они могут привести, но (2) не может присвоить исходам вероятности.

(Заметим, что многие теоретики считают, что все решения в условиях неизвестности можно преобразовать в рещения в условиях неуверенности. В таком случае этот раздел неважен, за исключением подраздела 6.1. Подробнее см. в разделе 7.)

6.1. Принцип доминирования

Заимствуем пример у Петерсона (2009, гл. 3). Предположим, что Джейн не знает, заказать ли в новом ресторане гамбургер или морского чёрта. Она знает, что в общем-то любой повар может приготовить съедобный гамбургер, а морской чёрт фантастически вкусен, если его готовил повар мирового класса, но готовить его сложно, и справится с этим не всякий. к сожалению, она слишком мало знает о ресторане, чтобы присвоить вероятность возможности, что морского чёрта приготовят хорошо. Её матрица принятия решений может выглядеть как-то так:

	Хороший повар	Плохой повар
Морской чёрт	Очень вкусно	Ужасно
Гамбургер	Съедобно	Съедобно
Ничего не заказывать	Остаться голодной	Остаться голодной

Тут в теоретики принятия решений говорят, что выбор «Гамбургер» доминирует над выбором Ничего не заказывать. Выбор гамбургера приводит к лучшим результатам для Джейн независимо от того, какое возможное состояние мира (хороший или плохой повар) оказалось истинным.

Этот принцип доминирования реализуется в двух вариантах:

• Слабое доминирование: Одно действие более рационально, чем другое, если (1) все его возможные исходы как минимум настолько же хороши, как у другого, и (2) Есть минимум один исход, который у первого действия лучше, чем у другого.
• Сильное доминирование: Одно действие более рационально, чем другое, если все его возможные исходы у первого действия лучше.

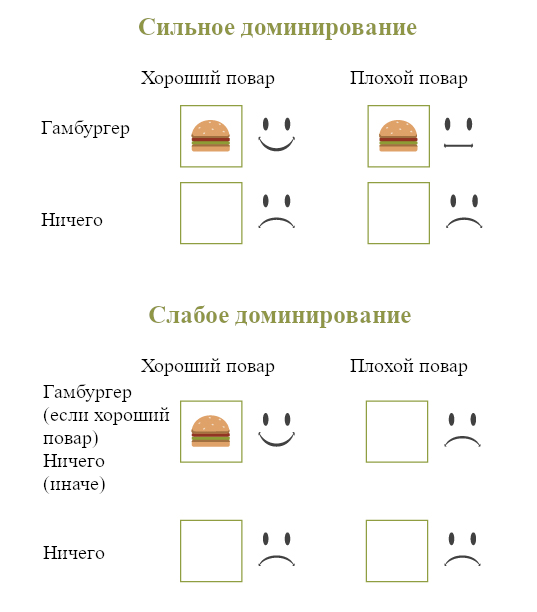
Сравнение сильного и слабого доминирования

Принцип доминирования можно применять и к решениям в условиях неуверенности (в которых всем исходам присвоены вероятности). Наличие вероятностей никак не отменяет того, что рационально предпочесть одно действие другому, если все исходы первого действия не хуже, чем у второго.

Впрочем, принцип доминирования бесспорно применим только к ситуациям, когда состояние мира независимо от действий агента. Рассмотри, например, такой выбор, украсть ли пальто:

	Арестовали	Не арестовали
Украсть	Тюрьма и пальто	Свобода и пальто
Не красть	Тюрьма	Свобода

В таком случае кража вроде-бы доминирует, но это вовсе не обязательно рациональное решение. В конце-концов, кража увеличивает шанс ареста, и это может сделать её плохим выбором. Так что доминирование неприменимо в подобных случаях, когда состояние мира не независимо от действия.

К тому же не во всех задачах принятия решений есть действие, доминирующее над всеми остальными. Так что для принятия таких решений нужны дополнительные принципы.

6.2. Максимин и лексимин

Некоторые теоретики предложили принцип максимина: если худший возможный результат одного действия лучше, чем худший возможный результат другого действия, следует предпочесть первый. В описанной выше задаче Джейн этот принцип предписывал бы выбрать гамбургер, потому что худший возможный результат там («Съедобно») лучше, чем худший возможный результат выбора морского чёрта («Ужасно»), и лучше, чем худший возможный результат выбора ничего не заказывать («Остаться голодной»).

Если худшие результаты двух или более действий одинаково хороши, то принцип максимина указывает быть между ними безразличными. Это не кажется правильным. Так что часто сторонники этого принципа расширяют его до лексическграфического принципа максимина («лексимин»), который утрвеждает, что если худшие исход двух или более действий одинаково хороши, то надо выбрать действие, у которого лучше второй по плохости исход. (Если и это не сужает выбор до одного действия, надо рассмотреть третий по плохости исход, и так далее.)

Какие есть аргументы в пользу принципа лексимина? Его сторонники указывают, что он преобразует задачу принятия решений в условиях неизвестности в задачу принятия решений в условиях частичной уверенности. Принимающий решение не знает, какой будет результат, но знает, какой может быть результат в худшем случае.

Но в некоторых случаях правило лексимина кажется явно иррациональным. Представьте такую задачу принятия решений с двумя возможными действиями и двумя возможными состояниями мира:

	s1	s2
a1	\$1	$10001.01
a2	\$1.01	\$1.01

В такой ситуации принцип лексимина предписывает выбрать a2. Но большинство людей согласится, что рационально рискнуть одним центом ради шанса получить лишние \$10000.

6.3. Максимакс и оптимизм-пессимизм

Правила максимина и лексимина обращают внимание на худший возможный исход решения, но почему бы не сосредоточиться на лучшем? Принцип максимакса предписывает предпочитать действие, у которого лучше лучший возможный вариант.

Более популярно правило оптимизма-пессимизма (также известное, как правило альфа-индекса). Оно предписыввает учитывать как лучший, так и худший возможный исход каждого действия, а потом выбирать согласно с своей степенью оптимизма или пессимизма.

Вот пример из Петерсона (2009, гл. 3):

	s1	s2	s3	s4	s5	s6
a1	55	18	28	10	36	100
a2	50	87	55	90	75	70

Мы отмечаем уровень оптимизма принимающего решение на шкале от 0 до 1, где 0 – это максимальный пессимизм, а 1 – максимальный оптимизм. У a₁ худший возможный исход – 10, а лучший – 100. Тогда если принимающий решение оптимистичен на 0.85, то ценность a₁ мы считаем равной (0.85)(100) + (1 - 0.85)(10) = 86.5, а ценность a₂ равной (0.85)(90) + (1 - 0.85)(50) = 84. В такой ситуации правильно оптимизма-пессимизма предписывает предпочесть действие a₁.

Если уровень оптимизма равен 0, то это правило сводится к принципу максимина, потому что (0)(max(a_i)) + (1 - 0)(min(a_i)) = min(a_i). А если уровень оптимизма равен 1, то правило сводится к принципу максимакса. Таким образом, это правило – обобщение и максимина, и максимакса. (Ну, в некотором роде. Минимакс и максимакс требуют изменения ценности лишь на ординальной шкале, а правило оптимизма-пессимизма уже требует интервальной.)

Правило оптимизма-пессимизма обращает внимание и на лучший, и на худший случаи, но рационально ли игнорировать всё посередине? Рассмотрим такой пример:

	s1	s2	s3
a1	1	2	100
a2	1	99	100

Максимальные и минимальные значения у a₁ и a₂ совпадают, так что они будут считаться эквиваленнтными независимо от степени оптимизма. Но кажется очевидным, что следует выбирать a₂.

6.4. Другие принципы принятия решений)

Для решений в условиях неизвестности предложено ещё много других принципов, включая минимакс сожаления (minimax regret), инфо-интервалы (info-gap), и максипок (maxipok). Подробнее о решениях в условиях неизвестности можно прочитать у Петерсона (2009) и Боссерта и пр. (2000).

Необычная черта обсуждённых в этом разделе принципов принятия решений – что они добровольно игнорируют часть ифнормации. Это может иеть смысл, если мы пытаемся найти алгоритм принятия решений, хорошо работающий в условиях сильно ограниченных вычислительных мощностей (Брафман и Тенненхольц (2000)), но не ясно, с чего бы идеальному агенту с бесконечной вычислительной мощностью (для нормативной, а не прескриптивной теории) добровольно пренебрегать информацией.

7. Можно ли преобразовывать решения в условиях неизвестности в решения в условиях неуверенности?

Могут ли решения в условиях неизвестности быть преобразованы в решения в условиях неуверенности? Это бы сильно всё упростило, потому что почти все согласны, что решения в условиях неуверенности следует обрабатывать «максимизацией ожидаемой полезности» (за разъяснениями см. раздел 11), а вот по поводу решений в условиях неизвестности ведутся споры.

С Байесианской (см. раздел 10) точки зрения, все решения в условиях неизвестности превращаются в решения в условиях неуверенности (Уинклер (2003), гл. 5) путём того, что принимающий решение устанавливает «априорную вероятность при неизвестности (ignorance prior)» каждому исходу, к которому неизвестно другого пути присвоить вероятность. (Можно выразиться по-другому – что Байесианский агент никогда не сталкивается с решениями в условиях неизвестности, потому что байесианец всегда должен присваивать событиям априорные вероятности.) Но надо установить, как именно их присваивать, а это важный источник споров среди байесианцев (см. раздел 10).

Многие не-байесианские теоретики тоже считают, что решения в условиях неизвестности можно преобразовать в решения в условиях неуверенности, благодаря так называемому принципы недостаточных причин. Он заключается в том, что если у вас нет буквально никаких причин считать одно состояние более вероятным, чем другое, то надо присвоить им равные вероятности.

Контраргумент против этого принципа – что он очень чувствителен к тому, как проводится разделение разных состояний. Петерсон (2009, гл. 3) объясняет:

Пусть вы отправляетесь в поездку и решаете, взять ли с собой зонт. [Но] вы ничего не знаете о погоде в вашем пункте назначения. Если формализация задачи принятия решения будет включать в себя лишь два состояния, с дождём и без дождя, [то, согласно принципу недостаточных причин] вероятность каждого будет 1/2. Однако, кажется, что с тем же успехом можно формализовать задачу так, что в ней будет три состояния, с ливнем, с слабым дождём и без дождя. Если принцип недостаточных причин применим и тут, то их вероятности будут по 1/3. В некоторых случаях эта разница повлияет на наше решение. Так что кажется, что если кто-то отстаивает принцип недостаточных причин, то он должен защищать и весьма неправдоподобную гипотезу, что есть ровно один правильный способ выбрать набор состояний.

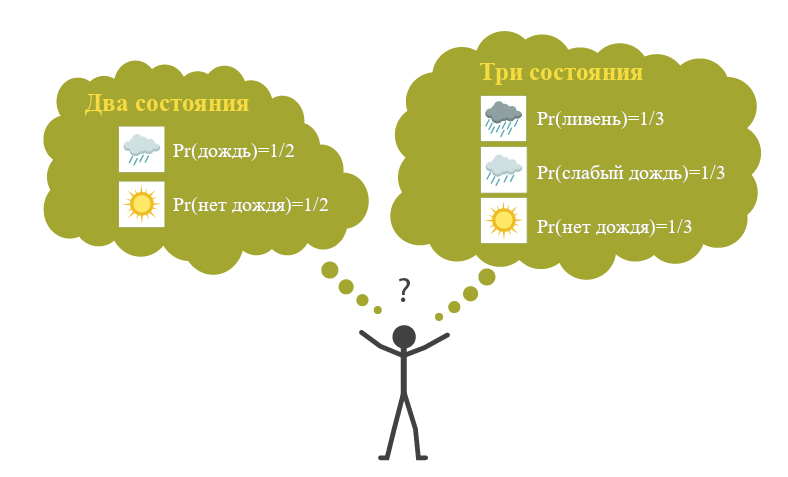
Возражение против принципа недостаточных причин

Сторонники принципа недостаточных причин могут ответить на это, что он касается симметричных состояний. Например, если кто-то дал вам игральную кость с n сторонами, и у вас нет причин считать, что она нечестная, то вам следует присвоить каждой стороне вероятность 1/n. Но Петерсон замечает:

…не все события можно описать в симметричных терминах. По крайней мере, не так, чтобы это оправдывало заключение о их равновероятности. Счастлива ли Энн в браке зависит от её будущего эмоционального отношения к её мужу. Согласно одному описанию, она либо будет его любить, либо не будет; тогда вероятность обоих состояний будет 1/2. Согласно другому, не менее правдоподобному, описанию, она может очень сильно его любить, немного его любить, или совсем его не любить. Тогда вероятность каждого состояния получается 1/3.

8. Как следует принимать решения в условиях неуверенности?

«Решение в условиях неуверенности» означает, что принимающий решение (1)знает, какие действия можно выбрать, и к каким исходам они могут привести, и (2) присваивает исходам вероятности.

В теории принятия решений в целом принят консенсус, что при столкновении с решением в условиях неуверенности рационально выбирать действие с наивысшей ожидаемой полезностью. Это принцип максимизации ожидаемой полезности (МОП).

Есть два разных обоснования МОП. Первое основывается на законе больших чисел (см. раздел 8.1). Второе использует аксиоматический подход (см. разделы с 8.2 по 8.5).

8.1. Закон больших чисел

«Закон больших чисел» устанавливает, что если вы достаточно долго снова и снова сталкиваетесь с одной и той же задачей принятия решений и всегда выбираете действие с наивысшей ожидаемой полезностью, то почти наверняка для вас это будет лучше, чем если бы вы выбирали любое другое действие.

У использования закона больших чисел для обоснования МОП есть две проблемы. Первая: мир всё время меняется, так что мы довольно редко, если вообще когда-либо, сталкиваемся с одной и той же задачей принятия решения «снова и снова». Закон больших чисел говорит, что если вы сталкиваетесь с одной и той же задачей бесконечно много раз, то вероятность, что вам лучше было бы не максимизировать ожидаемую полезность, стремится к нулю. Но вы никогда не будете сталкиваться с одной и той же задачей принятия решения бесконечно много раз! С чего вам волноваться о том, что произойдёт, если определённое условие будет выполняться, если вы знаете, что оно никогда не будет выполняться?

Вторая проблема связана с математической теоремой, известной как разорение игрока. Представьте, что мы с вами бросаем честную монетку, я плачу вам \$1 каждый раз, когда она выпадает решкой, а вы мне платите \$1 каждый раз, когда она выпадает орлом. Изначально у нас есть по \$100. Если мы бросим монетку достаточно много раз, то один из нас столкнётся с последовательностью орлов или решек, которую не может себе позволить. Если выпадет достаточно длинная цепочка решек, то у меня закончатся доллары, чтобы заплатить вам. Если выпадет достаточно долгая цепочка орлов, то вы не сможете заплатить мне. Так что в этой ситуации закон больших чисел гарантирует, что в конечном счёте максимизация ожидаемой полезности сделает вам лучше всего только если вы начали игру с бесконечным количеством денег (так что вы никогда не разоритесь), а это – нереалистичное допущение. (Для удобства предположим, что полезность линейна относительно денег. Но суть не меняется и без этого допущения.) [Прим. пер.: перевожу как есть, но я тоже не понимаю, в чём тут проблема. В итоге получается 50% на \$0 и 50% на \$200. Ожидаемые деньги – \$100, те же, как если не играть.]

8.2. Аксиоматический подход

Другой метод обоснования МОП стремится показать, что МОП можно вывести из аксиом, которые выполняются независимо от того, что происходит на бесконечности.

В этом разделе мы будем следовать, пожалуй, самому знаменитому аксиоматическому подходу от фон Неймана и Моргенштерна (1947). Есть и другие, например: Сэвидж (1954), Джеффри (1983), и Анскомб и Ауманн (1963).

8.3. Теорема о полезности фон Неймана – Моргенштерна

Впервые аксиоматическое обоснование теории принятия решений появилось в приложении к второму изданию Теории игр и экономического поведения (1947). Важно заранее заметить, что в этом аксиоматическом подходе за варианты, между которыми выбирает агент, фон Нейман и Моргентштерн взяли не действия как тут определили их мы, а «лотереи» (где лотерея – это множество исходов, каждому из которых сопоставлена вероятность). Так что, обсуждая их подход, мы тоже будем говорить о лотереях. (Хоть мы и проводим это различие, действия и лотереи тесно друг с другом связаны. В условиях неуверенности, с которыми тут работаем мы, каждое действие ассоциируется с своей лотереей, так что предпочтения между лотереями при желании можно использовать для определения предпочтений между действиями).

Ключевой элемент аксиоматического подхода фон Неймана и Моргенштерна – доказательство, что если агента есть предпочтения, определённые на множестве лотерей, и эти предпочтения удовлетворяют некоторому набору интуитивно-естественных структурных ограничений (аксиом), то мы можем сконструировать из этих предпочтений функцию полезности (с интервальной шкалой) и показать, что решения принимаются так, как будто агент максимизирует ожидаемую полезность согласно этой функции полезности.

Что это за аксиомы, которым должны соответствовать предпочтения агента о лотереях? Их четыре:

1. Аксиома полноты устанавливает, что агент должен озаботиться тем, чтобы установить предпочтение для каждой пары лотерей. То есть, агент должен предпочитать A по сравнению с B, или B по сравнению с A, или быть между ними безразличным.
2. Аксиома транзитивности устанавливает, что если агент предпочитает A по сравнению с B, а B по сравнению с C, то агент должен предпочитать и A по сравнению с C.
3. Аксиома независимости устанавливает, что, например, если агент предпочитает яблоко апельсину, то агент должен предпочитать и лотерею [55% получить яблоко, а иначе холеру] лотерее [55% получить апельсин, а иначе холеру]. И в общем случае, предпочтение должно сохраняться при вводе возможности получения нового исхода (напр., холеры).
4. Аксиома непрерывности устанавливает, что если агент предпочитает A по сравнению с B и B по сравнению с C, то существует одна конкретная вероятность p, такая что агент безразличен между [_p_(A) + (1 - p)(C)] и [точно исход B].

Аксиома непрерывности может потребовать дополнительных объяснений. Допустим, что A = \$1 млн., B = \$0 и C = Смерть. Если p = 0.5, это значит, что две лотереи, которые рассматривает агент, это:

1. (0.5)(\$1 млн.) + (1 - 0.5)(Смерть) [выиграть \$1 млн. с вероятностью в 50%, умереть с вероятностью в 50%]
2. (1)(\$0) [точно выиграть \$0]

Большинство людей не будут безразличны между \$0 и [50% шанс получить \$1 млн., 50% шанс погибнуть] — риск умереть слишком велик! Но если ваши предпочтения непрерывны, то есть какая-то вероятность p для которой вы были бы безразличны касательно двух таких лотерей. Вполне вероятно, что p очень, очень велика:

1. (0.999999)(\$1 мл.) + (1 - 0.999999)(Смерть) [выиграть \$1M с вероятностью 99.9999%, умереть с вероятностью 0.0001]
2. (1)(\$0) [точно выиграть \$0]

Возможно, теперь вы были бы безразличны между лотереей 1 и лотереей 2. Или, может быть, вы бы лучше рискнули смертью ради шанса выиграть \$1 млн., в каком случае p, для которого вы безразличны, ниже, чем 0.999999. Пока есть какое-то p, при котором вы будете безразличны между лотереями 1 и 2, ваши предпочтения «непрерывны».

Обосновываясь на этом фон Нейман и Моргенштерн доказали свою теорему, которая устанавливает, что если предпочтения агента между лотереями подчиняются этим аксиомам, то:

• Предпочтения агента могут быть представлены в виде функции полезности, которая присваивает более высокую полезность предпочитаемым лотереям.
• Агент действует в соответствии с принципом максимизации ожидаемой полезности.
• Все функции полезности, удовлетворяющие предыдущим двум условиям, являются «положительными линейными преобразованиями» друг друга. (Опуская подробности: поэтому VNM-полезность измеряется на интервальной шкале.)

8.4. Теория VNM-полезности и рациональность

Агента, соответствующего VNM-аксиомам, иногда называют «VNM-рациональным». Но с чего «VNM-рациональности» соответствовать нашему понятию рациональности вообще? Как этот результат о VNM-полезности обосновывает утверждение, что рациональный агент при столкновении с выбором в условиях неувренености будет максимизировать ожидаемую полезность? Рассуждения идут так:

1. Если агент (при решениях в условиях неуверенности) выбирает те лотереи, которые он предпочитает, и его предпочтения соответствуют VNM-аксиомам, то он рационален. Иначе, он иррационален.
2. Если агент (при решениях в условиях неуверенности) выбирает те лотереи, которые он предпочитает, и его предпочтения соответствуют VNM-аксиомам, то он максимизирует ожидаемую полезность.
3. Следовательно, рациональный агент при решениях в условии неуверенности максимизирует ожидаемую полезность.

Фон Нейман и Моргенштерн доказали посылку 2, а заключение 3 следует из посылок 1 и 2. Но почему следует принимать посылку 1?

Мало кто будет отрицать, что для агента было бы иррационально выбрать лотерею, которую он не предпочитает. Но почему иррационально чтобы предпочтения агента нарушали VNM-аксиомы? Я оставлю это обсуждения на раздел 8.6.

8.5. Возражения против VNM-рациональности

Результату фон Неймана и Моргенштерна предъявлялись некоторые возражения:

1. VNM-аксиомы слишком сильны. Некоторые заявляли, что VNM-аксиомы не самоочевидны. См. раздел 8.6.
2. VNM-система не даёт никакого руководства к действию. VNM-рациональный агент не может использовать теорию VNM-полезности как руководство к действию, потому что предпочтения касательно лотерей необходимо определить заранее. Но если агент может определить предпочтения касательно лотерей, то какую лотерею выбирать ему уже известно. (Больше об этом в разделе 9.)
3. В VNM-системе полезность определяется через предпочтения касательно лотерей, а не касательно исходов. Многим кажется странной идея определять полезность через предпочтения о лотереях. Много кто заявляет, что полезность надо определять относительно предпочтений об исходах или состояниях мира, а VNM-система делает не так. (Тоже см. раздел 9.)

8.6. Надо ли принимать VNM-аксиомы?

VNM-Аксиомы о предпочтениях определяют, что значит для агента быть VNM-рациональным. Но с чего нам их принимать? Обычно утверждается, что каждая из аксиом практически обоснована, потому что агент, который нарушает эти аксиомы, может столкнуться с ситуацией, в которой получит худший результат (с своей собственной точки зрения).

В разделах 8.6.1 и 8.6.2 я более подробно расскажут о практических обоснованиях, которые предлагаются для аксиом транзитивности и полноты. За большими подробностями, включая аргументы, обосновывающие две другие аксиомы, см. Петерсон (2009, гл. 8) и Ананд (1993).

8.6.1. Аксиома транзитивности

Рассмотрим аргумент выкачивания денег в пользу аксиомы транзитивности (если агент предпочитает A по сравнению с B, а B по сравнению с C, то агент должен предпочитать и A по сравнению с C).

Представьте, что друг предлагает вас ровно одну из трёх… книг, x или y или z… [и] что ваши предпочтения касательно этих трёх книг… [такие, что] вы предпочитаете x по сравнению с y, y по сравнению с z, и z по сравнению с x… [То есть, ваши предпочтения зациклены и ваше отношение предпочтения не транзитивно.] Теперь представьте, что у вас есть книга z, и вам предложили поменять z на y. Поскольку вы предпочитаете y по сравнению с z, рационально поменяться. Так что вы меняетесь, и временно получаете y. Затем, вам предлагают поменять y на x, и вы соглашаетесь, потому что предпочитаете x по сравнению с y. Наконец, вам предложили чуть-чуть заплатить, скажем, один цент, за обмен x на z. Поскольку z строго [предпочитается по сравнению с] x, даже после того, как вы заплатили за обмен, рационально принять предложения. Получается, вы оказались там же, где и начинали, с разницей только, что теперь у вас на цент меньше. Дальше эта процедура повторяется снова и снова. После миллиарда циклов вы потеряли десять миллионов долларов, ничего не получив взамен. (Петерсон (2009), гл. 8)

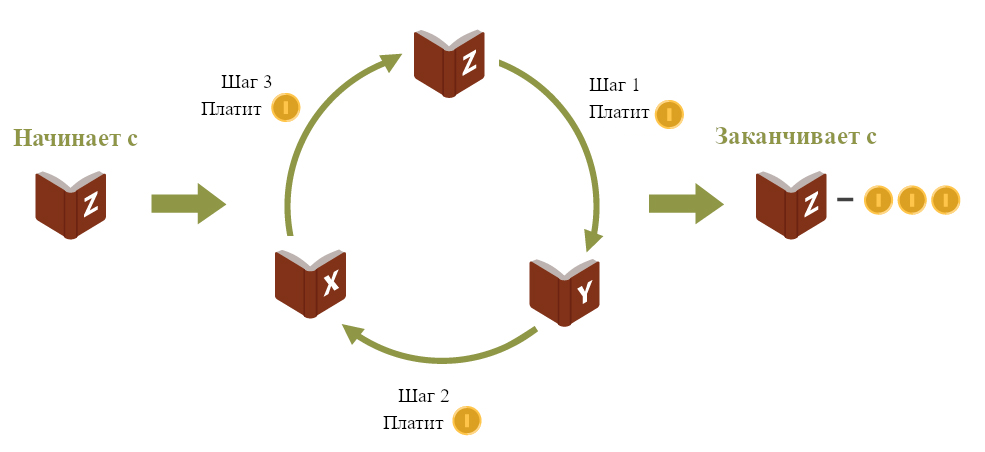
Пример аргумента от выкачивания денег

Аналогичные аргументы (напр., Густавсон 2010) стремятся показать, что и другие виды нетранзитивных/ациклических предпочтений тоже иррациональны.

(Конечно, практические аргументы не обязаны формулироваться в денежных терминах. Мы с тем же успехом могли бы сконструировать аргумент, показывающий, что из агента с нетранзитивными предпочтениями можно «выкачать» всё счастье, все моральные добродетели или все печеньки.)

8.6.2. Аксиома полноты

Аксиому полноты («агент должен предпочитать A по сравнению с B, или B по сравнению с A, или быть между ними безразличным») часто критикуют, заявляя, что некоторые блага или исходы несравнимы. Например, должен ли рациональный агент высказывать предпочтение (или безразличие) между деньгами и человеческим благополучием?

Вероятно, аксиому полноты можно обосновать практическими аргументами. Если вы считаете, что рационально-допустимо обменивать несравнимые ценности, то можно сконструировать аргумент от выкачивания денег, обосновывающий полноту. Но если вы считаете, что обменивать несравнимые блага не рационально, то такого аргумента составить не получится. (На самом деле, даже если считать, что это рационально, в Мэндлер, 2005 показано, что если агент позволяет новым выборам зависеть от предыдущих, он может избежать выкачивания денег.

На самом деле, есть популярный аргумент против аксиомы полноты: «аргумент о маленьком улучшении». Подробнее см Ченг (1997) и Эспиноза (2007).

Замечу, что теория выявленных предпочтений, согласно которой предпочтения выявляются через поведение при выборах, не оставляет места для несравнимых предпочтений, потому что каждый выбор всегда выявляет отношение предпочтения «лучше, чем», «хуже, чем» или «равно хорошо».

Ещё для того, чтобы разобраться с кажущейся несравнимостью некоторых благ (вроде денег и человеческого благополучия) предлагают мультиатрибутный подход:

В мультиатрибутном подходе каждый атрибут измеряется лучше всего подходящей для него единицей изменения. Может, для финансовых затрат это деньги, а для человеческого благополучия – число спасённых жизней. Общая ценность альтернативы тогда определяется сбором из атрибутов, т.е. денег и жизней, общей сравнительной оценки…

Для выбора из альтернатив с несколькими атрибутами предложено несколько критериев… [Например,] аддитивный критерий присваивает каждому атрибуту вес и сравнивает их по взвешенным суммам, полученным перемножением веса каждого атрибута на его значение. [Хоть] это, пожалуй, и спорно – измерять полезность очень разных объектов на общей шкале… равно спорным кажется и присваивать атрибутам численные веса, как предлагается тут…

[Теперь давайте] рассмотрим очень общее возражение мультиатрибутным подходам. Согласно этому возражению, существует несколько правдоподобных, но разных способов сконструировать список атрибутов. Иногда исход процесса принятия решений зависит от того, какой набор атрибутов выбран. (Петерсон (2009), гл. 8)

Подробнее о мультиатрибутном подходе см. Кини и Райффа (1993).

8.6.3. Парадокс Алле

Мы рассмотрели аксиомы транзитивности и полноты. Теперь мы можем перейти к аксиоме независимости (предпочтение должно сохраняться при вводе возможности получения нового исхода). Есть ли причины её отвергнуть? Вот один повод считать, что может и есть, известный как парадокс Алле (Алле (1953)). Может казаться разумным действовать так, что это противоречит независимости.

Парадокс Алле предлагает нам рассмотреть два выбора (эта версия парадокса основана на Юдковском (2008)). Первый – выбор между:

(1A) получить \$24,000; и (1B) шанс 33/34 получить \$27,000 и 1/34 ничего не получить.

Второй – выбор между:

(2A) шанс 34% получить \$24,000 и 66% шанс ничего не получить; и (2B) шанс 33% получить \$27,000 и шанс 67% ничего не получить.

Эксперименты показали, что многие люди предпочитают (1A) по сравнению с (1B) и (2B) по сравнению с (2A). Но такие предпочтения противоречат независимости. 2A – то же самое, что [шанс 34% получить 1A и шанс 66% ничего не получить] а 2B – то же самое, что [шанс 34% получить 1B и шанс 66% ничего не получить]. Так что независимость требует, чтобы предпочитающие (1A) по сравнению с (1B) предпочитали (2A) по сравнению (2B).

Когда этот результат был получен впервые, его приводили как свидетельство против аксиомы независимости. Однако, хоть парадокс Алле, безусловно, показывает, что независимость не выполняется для дескриптивной теории, совсем неочевидно, что он что-то говорит о нормативном представлении рационального выбора, которое мы тут обсуждаем. Впрочем, как отмечено у Петерсона (2009, гл. 4):

Раз многие, кто много думал об этом примере, всё ещё считают, что было бы рациональным придерживаться описанного выше проблематичного набора предпочтений, кажется, с принципом ожидаемой полезности что-то не так.

Но затем Петерсон отмечает, что многие другие, например, статистик Леонард Сэвидж, считают, что ошибка в парадоксе Алле в человеческих предпочтениях, а не в аксиоме независимости. Если так, то парадокс, кажется, демонстрирует опасность излишнего полагания на интуицию при определении того, как должна выглядеть нормативная теория рациональности.

8.6.4. Парадокс Эллсберга

Парадокс Алле – далеко не единственный случай, когда люди не ведут себя в соответствии с МОП. Другой широко известный пример – парадокс Эллсберга (дальше описан согласно Резнику (1987):

В урне перемешаны девяносто шаров одинакового размера. Тридцать шаров жёлтые, а оставшиеся шестьдесят красные или синие. Нам неизвестно, сколько красных/синих шаров в урне, кроме того, что это число от нуля до шестидесяти. Теперь рассмотрим две ситуации. В каждой ситуации втаскивается шар, и нам надо сделать ставку на его цвет. В ситуации A мы выбираем между ставкой на то, что он жёлтый, и на то, что он красный. В ситуации B мы выбираем между ставкой на то, что он красный или синий, и ставкой на то, что он жёлтый или синий.

Если игрок угадывает, он получает \$100. Парадокс Эллсберга заключается в том, что многие люди ставит на жёлтый в ситуации A и на красный или синий в ситуации B. Более того, многие принимают такие решения не потому, что в обеих ситуациях безразличны, а, скорее, потому, что у них есть строгое предпочтение выбирать именно так.

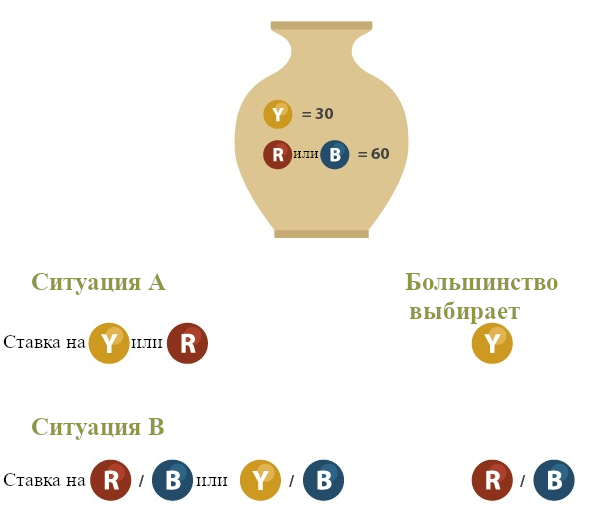
Парадокс Эллсберга

Но такое поведение не может соответствовать МОП. Чтобы МОП одобряла строгое предпочтение выбора жёлтого в ситуации A, агент должен присваивать тому, что выбранный шар будет синим, вероятность выше 1/3. Напротив, чтобы МОП одобряла выбор красного или синего в ситуации B, агент должен присваивать тому, что выбранный шар будет синим, вероятность ниже 1/3. Так что совместно эти решения агент, следующий МОП, принимать не будет.

Те, кто считает, что решения в условиях неизвестности нельзя преобразовать в решения в условиях неуверенности, с лёгкость. отвечают на парадокс Эллсберга: этот пример использует ситуацию в условиях неизвестности, так что то, что решения людей нарушают МОП не имеет значения, потому что она тут всё равно неприменима.

Тем же, кто считает, что МОП – подходящий стандарт для выбора в таких ситуациях, надо найти другой ответ на парадокс. Как и с парадоксом Алле есть некоторые разногласия по поводу того, какой ответ лучше. Впрочем, и тут многие, включая Леонарда Сэвиджа, заявляют, что МОП тут приводит к правильному решению, и это наша интуиция ошибается (за хорошим пересказом аргументов Сэвиджа опять см. Resnik (1987).

8.6.5. Санкт-Петербургский парадокс

Другое возражение против подхода VNM (и в целом против ожидаемой полезности) – это Санкт-Петербургский парадокс. Он использует бесконечные полезности. Он основан на игре, в которой подбрасывают честную монетку до тех пор, пока она не упадёт орлом. В этот момент агент получает приз в 2ⁿ полезности, где n – это число произошедших подбрасываний. Так называемый парадокс получается потому, что ожидаемая полезности выбора сыграть в эту игру бесконечно, так что, согласно стандартному подходу ожидаемой полезности, за право сыграть агент должен быть согласен заплатить любую конечную цену. Но это кажется неразумным. Скорее кажется, что агент должен быть готов заплатить сравнительно немного. Так что опять получается впечатление, что подход ожидаемой полезности тут ошибочен.

На это отвечали по-разному. Самое очевидное – мы можем сказать, что парадокс неприменим к VNM-агентам, потому что теорема VNM присваивает всем лотереям вещественные числа, а бесконечность – не вещественное число. Но неочевидно, что это решает всю проблему. В конце-концов, Санкт-Петербургский парадокс по сути своей не о бесконечных полезностях, а о случаях, когда подход ожидаемой полезности, кажется, переоценивает какой-то из вариантов. Такие случаи можно сконструировать и в конечном случае. Например, если L будет конечным ограничением полезности, то можно рассмотреть такой сценарий (из Петерсона, 2009, p. 85):

Честную монетку подбрасывают, пока она не упадёт орлом. Потом игрок получает приз в min{2n·10^-100, L} единиц полезности, где n – число произошедших подбразываний монетки.

В таком случае, даже если L велика, кажется, что много платить за право сыграть неразумно. В конце-концов, как замечает Петерсон, в девяти случаях из десяти игрок выиграет не больше 8·10^-100. Если тут и правда неразумно заплатить 1 единицу полезности, то простого ограничения полезности агента неким конечным количеством не хватит, чтобы защитить подход ожидаемой полезности. (Есть и другие проблемы. см. интересную конечную проблему у Юдковского, 2007 и особо озадачивающий пример, связанный с Санкт-Петербургским парадоксом, у Новера и Хайека, 2004)

Как обычно, нет консенсуса по поводу того, что выявляет Санкт-Петербургский парадокс. Некоторые принимают одно из решений и не беспокоятся по его поводу. Другие считают, что он выявляет серьёзную проблему с теориями ожидаемой полезности. Третьи считают, что парадокс не разрешён, но забрасывать теорию ожидаемой полезности всё равно не надо.

9. Даёт ли аксиоматическая теория принятия решений хоть какое-то руководство к действию?

Часто утверждается, что для теорий, перечисленных в разделе 8.2 ответ «нет». Чтобы объяснить получше, я сначала опишу некоторые различия между прямым и косвенным подходами к аксиоматической теории принятия решений.

Петерсон (2009, гл. 4) объясняет:

При косвенном подходе, а он наиболее популярен, агент предпочитает рискованное действие [или лотерею] в сравнении с другим не потому что ожидаемая полезность первого выше. Нет, агента просто просят высказать предпочтения касательно некоторого множества рискованных действий… Затем, если эти предпочтения соответствуют небольшому набору структурных ограничений (аксиом), то можно показать, что решения агента можно описать так, как будто бы агент выбирал, что делать, присваивая исходам численные вероятности и полезности и затем максимизируя ожидаемую полезность…

[В противовес этому,] прямой подход стремится построить предпочтения по поводу действий из напрямую присвоенных исходам вероятностей и полезностей. В отличие от косвенного подхода, нет допущения о том, что у агента есть доступ к предпочтениям до этих рассуждений.

Все аксиоматические теории принятия решений, перечисленные в разделе 8.2, следовали косвенному подходу. Можно сказать, что эти теории не могут выдать никакого руководства к действию, потому что они требуют, чтобы агент «заранее» установил свои предпочтения. Но агент, который их уже установил, уже знает, что предпочитает, так что теория не может дать ему нового руководства к действию, которого у него уже не было в предпочтениях.

Петерсон (2009, гл. 10) приводит практический пример:

Например, сорокалетняя женщина, которая хочет совета по поводу, скажем, того, развестись ли ей с мужем, вероятно, получит [от двух подходов] очень разные ответы. [Косвенный подход] посоветует ей сначала выяснить собственные предпочтения по поводу очень большого набора рискованных действий, включая те, о которых она изначально задумывается, а потом просто увериться, что все её предпочтения совместимы с определёнными структурными требованиями. Затем, пока эти требования не нарушены, женщина может делать что ей угодно, независимо от того, какие у неё на самом деле убеждения и желания. [Прямой подход] же посоветует ей сначала присвоить её желаниям и убеждениям численные полезности и вероятности, а потом аггрегировать их в решение, применив принцип максимизации ожидаемой полезности.

Выходит, только прямой подход даёт агенту руководство к действию. Но прямой подход очень молод (Петерсон (2008); Козик (2011)), и только время покажет, выдержит ли он испытание профессиональной критикой.

Предупреждение: Может запутать то, что прямой подход Петерсона (2008) называется «не-Байесианской теорией принятия решений», несмотря на то, что он использует Байесианскую теорию вероятности.

За другими попытками получить руководство к действию из нормативной теории принятия решений, см. Фалленштейн (2012) и Стиннон (2013).

10. Какую роль в теории принятия решений играет теория вероятности?

Чтобы рассчитать ожидаемую полезность действия (или лотереи) необходимо определить вероятность каждого исхода. В этом разделе я пройдусь по элементам теории вероятности, связанным с теорией принятия решений.

За дополнительными вводными материалами в теорию вероятности, см. Хаусон и Урбах (2005), Гриммет и Стирзакер (2001), и Кллер и Фридман (2009). Этот раздел сильн заимствует из Петерсона (2009, гл. 6 & 7), где приводится очень ясное введение в вероятности в контексте теории принятия решений.

10.1. Основы теории вероятности

Интуитивно, вероятность – это число между 0 и 1, обозначающее, насколько возможно наступление некоторого события. Если у события вероятность 0, то оно невозможно. А если у события вероятность 1, то оно не может не произойти. Есть вероятность события где-то посередине, то событие тем вероятнее, чем выше это число.

Как и с МОП, теорию вероятности можно вывести их небольшого набора простых аксиом. В случае вероятности, их три. Они называются аксиомами Колмогорова в честь советского математика Андрея Колмогорова. Первая аксиома устанавливает, что вероятности – это вещественные числа между 0 и 1. Вторая – что если события в некотором множестве взаимоисключающи и при этом исчерпывающи (то есть, точно произойдёт ровно одно из них), то сумма вероятностей этих события должна быть равна 1. Третья – что есть два события взаимоисключающи, то вероятность, что произойдёт одно из них, равна сумме их отдельных вероятностей.

Из этих трёх аксиом можно вывести всю остальную теорию вероятности. Дальше в этом разделе я пройдусь по некоторым элементам этой широкой теории.

10.2. Теорема Байеса для обновления вероятностей

Для теории принятия решений особо важным элементом теории вероятности является идея условных вероятностей. Они соответствуют тому, насколько что-то вероятно при учёте некоторой дополнительной информации. Так что, например, условная вероятность может показывать, насколько возможно, что будет дождь, при условии, что прогноз погоды его предсказал. Мощный инструмент для вычисления условных вероятностей – теорема Байеса (см. более подробное введение у Юдковского, 2003). Формула такова:

P(A|B)=(P(B|A)P(A))/P(B)

Теорему Байеса используют, когда надо вычислить вероятность некоторого события A при наличии свидетельства B. Так что эта формула используется для обновления вероятностей на основе новых свидетельств. Пусть вы пытаетесь оценить вероятность того, что завтра будет дождь, и кто-то сообщил вам, что прогноз погоды предсказал, что будет. Эта формула скажет вам, как вычислить новую вероятность на основе новой информации. В подобных случаях изначальную вероятность (до учёта новой информации) называют априорной, а новую вероятность, получившуюся в результате применения теоремы Байеса – апостериорной.

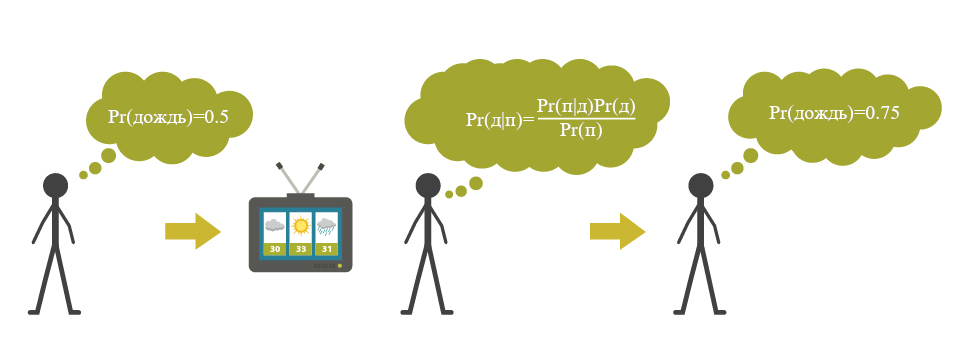
Использование теоремы Байеса для обновления вероятности на основе свидетельства от прогноза погоды.

Теорема Байеса, кажется, решает задачу обновления априорных вероятностей на основе новой информации. Но она оставляет открытым вопрос о том, как изначально определить априорную вероятность. Иногда нет очевидного способа это сделать. Одно из предложенных решений этой проблемы – выбрать любые осмысленные априорные вероятности. Если набрать достаточно свидетельств, то многократное применение теоремы Байеса сведёт вероятности к примерно одним и тем же апостериорным, даже при очень разных стартовых точках. Так что изначальный выбор не настолько критически важен, как может показаться.

10.3. Как вероятности следует интерпретировать

Есть две основных точки зрения на то, что значат вероятности: объективизм и субъективизм. Грубо говоря, объективисты считают, что вероятности говорят нам что-то о внешнем мире, а субъективисты – что они говорят нам о наших убеждениях. В теории принятия решений большинство придерживается субъективистских взглядов на вероятности. Согласно ним в вероятностях представлены субъективные степени убеждённости. То есть, сказать, например, что вероятность дождя равна 0.8 – это сказать, что агент, о котором идёт речь, довольно сильно убеждён, что пойдёт дождь (см. обоснования этой точки зрения в Jaynes, 2003). Заметим, что, согласно этому взгляду, другой агент в тех же обстоятельствах мог бы присвоить тому, что пойдёт дождь, другую вероятность.

10.3.1. С чего степеням убеждённости следовать законам о вероятностях?

Против субъективной точки зрения на вероятности можно высказать вопрос: почему, в таком случае, наши степени убеждённости обязаны соответствовать аксиомам Колмогорова? Например, почему наши субъективные степени убеждённости в взаимоисключающие исчерпывающие события должны складываться в единицу? На это можно ответить, например, что агенты, чьи степени убеждённости не соответствуют этим аксиомам, будут уязвимы для предложений ставок с гарантированным проигрышем. Петерсон (2009, гл. 7) разъясняет:

Например, допустим, что вы убеждены, что хотя бы один индус выиграет золотую медаль на следующих Олимпийских Играх (событие G) с степенью 0.55. И, в то же время, ваша субъективная степень убеждённости в том, что ни один индус не выиграет золотую медаль на следующих Олимпийских Играх (событие ¬G) равна 0.52. И пусть тогда хитрый букмекер предлагает заплатить вам \$1 за каждое из этих событий, которое реально произойдёт. Тогда, так как ваша субъективная степень убеждённости, что произойдёт G равна 0.55, рационально было бы заплатить за ставку на это вплоть до \$1·0.55 = \$0.55. Но более того, раз ваша степень убеждённости в ¬G равна 0.52, вы должны быть готовы заплатить вплоть до \$0.52 за право сделать ставку и на второе событие, ведь \$1·0.52 = \$0.52. Но теперь получается, что вы заплатили \$1.07 за совершение двух ставок, которые точно принесут вам ровно \$1 независимо от того, что произойдёт… Уж точно это должно быть иррациональным. Причина иррациональности – то, что ваши субъективные степени убеждённости нарушали законы вероятности.

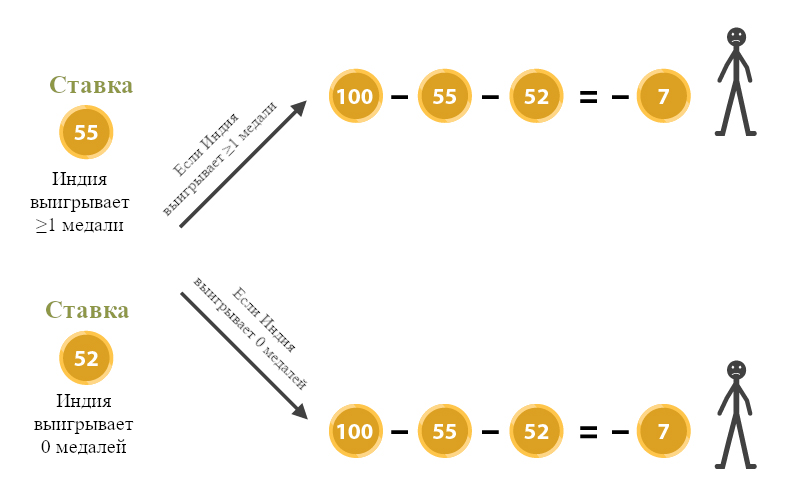
Аргумент от ставок

Можно доказать, что агент уязвим для подобных систем ставок тогда и только тогда, когда его степени убеждённости нарушают аксиомы вероятности. Это обосновывает, почему степени убеждённости должны им соответствовать.

10.3.2. Измерение субъективных вероятностей

Другая сложность для субъективного подхода – как вероятности измерять. Если они представляют субъективные степени убеждённости, то, кажется, нет простого способа их определить, основываясь на наблюдениях за миром. Но на эту проблему появляется всё больше ответов, один из которых лаконично описан у Петерсона (2009, гл. 7):

Главное новшество… Сэвиджа можно охарактеризовать как систематические процедуры для связи вероятности… с утверждениями об объективно наблюдаемом поведении, например, за предпочтениями, выявленными выбором. Например, представьте, что мы хотим измерить субъективную вероятность, которую Кэролин присваивает тому, что монетка у неё в руках при следующем подбрасывании упадёт орлом. Для начала, мы спросим у неё, какой из таких двух весьма щедрых вариантов она бы предпочла:

A: «Если монета упадёт орлом, ты выигрываешь автомобиль, а иначе – ничего.»

B: «Если монета не упадёт орлом, ты выигрываешь автомобиль, а иначе – ничего.»

Предположим, Кэролин предпочитает A. Тогда мы можем заключить, что она считает, что монетка вероятнее упадёт орлом, чем нет. Для этого надо сделать допущения, что Кэролин предпочитает выиграть автомобиль, а не ничего, и что её предпочтения по поводу таких предложений в условиях неуверенности полностью определяются её убеждениями и желаниями, касающимися перспективы выиграть автомобиль…

Наконец, нам надо обобщить обрисованную выше процедуру измерения, чтобы она всегда позволяла нам представить степени убеждённости Кэролин в виде точных численных вероятностей. Для этого нам понадобится попросить Кэролин высказать предпочтения касательно куда большего множества вариантов, а потом решать с конца… Например, допустим, что Кэролин хочет измерить свою субъективную вероятность того, что её машина, стоящая \$20,000 будет украдена в течении года (событие S). Если она считает, что \$1000 – это… самая высокая цена, которую она готова заплатить за то, что в случае наступления события S она получит \$20000, то получается, что субъективная вероятность S у Кэролин равна 1000/20000 = 0.05. Это при условии, что её предпочтения соответствуют принципу максимизации ожидаемой денежной ценности…

Проблема с этим методом – что очень мало у кого предпочтения сформированы соответственно принципу максимизации ожидаемой денежной ценности. Для большинства людей добавочная полезность денег падает с их количеством…

К счастью, [у этой проблемы] есть умное решение. Основная идея – поставить на предпочтения по поводу вариантов выборов в условиях неуверенности некоторые структурные ограничения [напр., аксиому транзитивности]. Тогда субъективная функция вероятности получается при их учёте сама собой, как бы задним числом. Раз агент в условиях неуверенности предпочитает одни варианты другим, и его предпочтения… соотвествуют структурным аксиомам, то агент ведёт себя так, будто предпочтения формируются через присвоение субъективных вероятностей и полезностей и последующую максимизацию ожидаемой полезности.

Любопытная черта этого подхода – что вероятности (и полезности) выводятся «изнутри» теории. Агент в условиях неуверенности предпочитает один вариант другому не потому что считает субъективные вероятности и полезности первого более привлекательными. Скорее… из структуры предпочтений агента логически вытекает, что их можно описать так, как будто выбор агента руководствуется субъективными функциями вероятности и полезности…

…Сэвидж стремится выявить субъективные интерпретации аксиом вероятности, утверждая что-то о предпочтениях… в условиях неуверенности. Но… с чего бы теории субъективной вероятности использовать какие-то допущения о предпочтениях? Предпочтения и убеждения – разные вещи. Что бы там ни говорили [Сэвидж и прочие], лишённый всяких эмоций и предпочтений агент всё равно точно мог бы обладать какими-то убеждениями.

Есть и другие подходы, например, вот из DeGroot (1970):

Основное допущение ДеГрута – что агент может качественно сравнивать пары событий, судить, какое из них более вероятно. Например, можно допустить, что агент может решить для себя, более, менее или равновероятно, согласно его убеждениям, то, что пойдёт дождь в Кембридже, по сравнению с тем, что пойдёт дождь в Каире. Дальше ДеГрут показывает, что если качественные суждения агента достаточно аккуратны и удовлетворяют нескольким структурным аксиомам, то [их можно описать распределением вероятностей]. Так что в теории ДеГрута – функция вероятности выстраивается аккуратными качественными оценками, что делает их количественными.

11. Что насчёт «задачи Ньюкомба» и альтернативных алгоритмов принятия решений?

К сожалению, сказать, что рациональный агент «максимизирует ожидаемую полезность» – недостаточно конкретно. Есть больше одного алгоритма принятия решений, стремящегося максимизировать ожидаемую полезность, и эти алгоритмы дают разные ответы на некоторые задачи. «Задача Ньюкомба» – одна из таких.

В этом разделе мы рассмотрим эти алгоритмы и покажем, как они работают на задаче Ньюкомба и в похожих «ньюкомбоподобных» случаях.

Некоторые из основных источников на эту тему: Кэмпбелл и Соуден (1985), Ледвиг (2000), Джойс (1999), и Юдковский (2010). Мёртельмайер (2013) обсуждает ньюкомбоподобные задачи в контексте систем «агент-окружение».

11.1. Ньюкомбоподобные задачи и два алгоритма принятия решений

Я начну с представления нескольких ньюкомбоподобных задач, чтобы потом я мог к ним обращаться. Ещё я ознакомлю вас с нашими первыми двумя алгоритмами принятия решений, чтобы я мог демонстрировать, как выбор алгоритма влияет на результаты, которых добивается агент в этих задачах.

11.1.1. Задача Ньюкомба

Эту задачу сформулировал физик Уильям Ньюкомб, а впервые опубликаована она была в Нозик (1969). Ниже я опишу её версию, вдохновлённую Юдковским (2010).

Суперинтеллектуальный робот под именем Омега из другой галактики посещает Землю и демонстрирует, что он очень хорош в предсказании событий. Тут нет никакой магии, просто он куда больше нас знает о науке, у него есть миллиарды сенсоров, раскиданных по всей планете, и вычислительный кластер размером с Луну, на котором он использует эффективные алгоритмы для моделирования людей и других сложных систем с беспрецедентной точностью.

Омега показывает вам две коробки. Коробка A прозрачная, и в ней лежит \$1000. Коробка B непрозрачная, и либо в ней лежит \$1 млн., либо она пуста. Вы можете выбрать взять обе коробки или взять только коробку B. Если Омега предсказал, что вы возьмёте обе коробки, то он оставил коробку B пустой. А вот если Омега предсказал, что вы возьмёте только одну коробку, то он положил в коробку B миллион.

К тому моменту, как вам представлен выбор, Омега уже улетел играть в следующую игру. Содержимое коробки B не изменится после того, как вы примете решение. Более того, вы уже видели, как Омега играл в подобные игры с подобными вам людьми тысячу раз, и он всегда предсказывал выбор игрока правильно.

Стоит брать одну коробку или две:

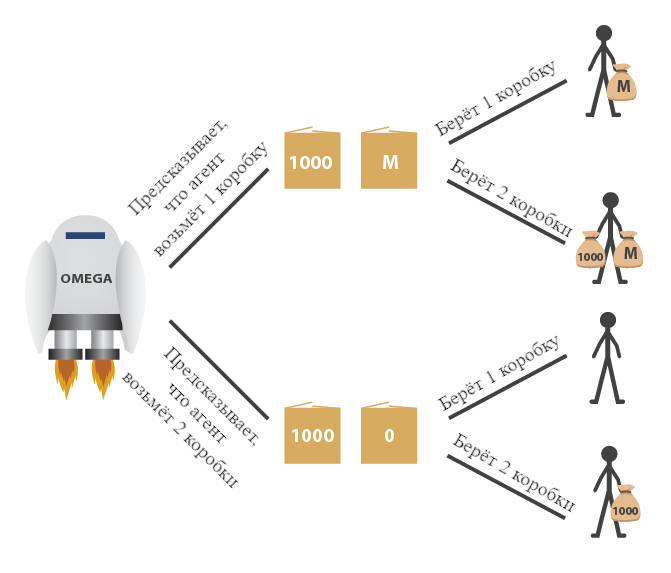
Задача Ньюкомба

Вот аргумент за то, чтобы брать две коробки. Либо миллион в коробке уже есть, либо его там уже нет. Ваш выбор сейчас не может повлиять на содержимое коробки B. Поэтому, вам надо брать две коробки, потому что тогда вы получаете тысячу долларов плюс то, что в коробке B. Это прямое применение принципа доминирования (раздел 6.1). Выбор двух коробок доминирует над выбором одной.

Убеждены? Ну а вот аргумент за выбор одной коробки. Во всех тех играх, которые вы раньше видели, все, кто брал две коробки, получали тысячу долларов, а все, кто брал одну – получали миллион. Так что вы практически уверены, что взяв две коробки получите тысячу, а взяв одну – миллион. Так что, чтобы максимизировать свою ожидаемую полезность, вам надо взять одну коробку.

Нозик (1969) сообщает:

Я задавал эту задачу многим людям… Почти для всех совершенно ясно и очевидно, что надо делать. Сложность в том, что эти люди почти поровну разделились во мнениях, и многие из них считают, что другая половина просто говорят глупости.

Это не «лишь вербальный» спор (Chalmers 2011). Теория принятия решений предлагает несколько алгоритмов совершения выбора, и они приводят к разным исходам. Если перевести на простой язык, первый алгоритм, «свидетельственная теория принятия решений» (evidential decision theory, EDT, СТПР) говорит: «Выбирай такие действия, что ты был бы рад получить новость о том, что ты их выбрал». Второй алгоритм, «каузальная теория принятия решений» (causal decision theory, CDT, КТПР) говорит: «Выбирай такие действия, от которых ты ожидаешь позитивного воздействия на мир».

У многих теоретиков интуиция поддерживает правоту CDT. Но CDT-агент «проигрывает» в задаче Ньюкомба, остаётся с тысячей долларов, тогда как EDT-агент получает миллион. Сторонники EDT могут спросить сторонников CDT: «Если вы такие умные, то почему такие бедные?». Как пишет Спон (2012), «это должна быть плохая рациональность, если она возмущается о вознаграждении иррациональности.» Или как утверждает Юдковский (2010):

Максимизатор ожидаемой полезности должен максимизировать полезность – не формальность, разумность или недоступность критике…

В ответ на явную «победу» EDT над CDT в задаче Ньюкомба, сторонники CDT представили аналогичные задачи, в которых CDT-агент «выигрывает», а EDT-агент «проигрывает». Сторонники EDT же ответили дополнительными ньюкомбоподобными задачами, в которых снова EDT выигрывает, а CDT проигрывает. Давайте рассмотрим их по очереди.

11.1.2. Свидетельственная и каузальная теории принятия решений

Но для начала немного подробнее рассмотрим наши два алгоритма принятия решений.

EDT описать легко: согласно этой теории, для определения ожидаемой полезности разных действий агентам следует использовать условные вероятности. Конкретнее, им надо использовать вероятность того, что мир находится в каждом возможном состоянии, при учёте рассматриваемого действия. Так что в задаче Ньюкомба они рассматривают вероятность того, что коробка B содержит миллион, при условии свидетельства, что они приняли решение взять одну или две коробки. Так теория формализует «действие – хорошие новости».

CDT сложнее, как минимум потому, что её формулировали многими разными способами, и они эквивалентны друг другу только при принятии некоторых фоновых допущений. Хорошо помогает её понять рассмотрение подхода через контрфактуалы. Это одна из наиболее интуитивно понятных формулировок. Этот подход использует вероятности при определённых гипотетических условиях. Можно считать, что они отображают каузальное воздействие выбора агента на состояние мира, вроде «если бы я выбрал определённое действие, то мир был бы в таком-то состоянии». В задаче Ньюкомба такая формулировка CDT рассматривает вероятность контрфактуалов вроде «если бы я взял одну коробку, то в коробке B был бы миллион» и так оценивает каузальное воздействие выбора на содержимое коробок.

Можно провести это различие и в формулах. EDT и CDT обе согласны, что следует максимизировать ожидаемую полезность действия, где ожидаемая полезность действия A_i при множестве возможных исходов O определена так:

В этом уравнении V(A_i & O_j) – это ценность для агента сочетания действия и исхода. То есть, это полезность, которую получает агент, если совершает определённое действие с определённым исходом. А Pr_AiO_j – это вероятность наступления исхода O_j при условии того, что агент выбрал действие A_i. Именно в этой вероятности CDT и EDT различаются. EDT использует условную вероятность, Pr(O_j|A_i), а CDT – гипотетическую вероятность Pr(A_i□→O_j).

Эти две версии формулы ожидаемой полезности позволяют формально продемонстрировать, почему EDT и CDT дают свои ответы на задачу Ньюкомба. Давайте примем два упрощающих допущения. Во-первых, что для агента каждый доллар стоит ровно одну единицу полезности (так что для него полезность денег линейна). Во-вторых, что Омега – идеальный предсказатель действий людей, так что если агент берёт две коробки – это однозначное свидетельство, что в непрозрачной коробке ничего нет, и наоборот. При этих допущениях, EDT вычисляет ожидаемую полезность каждого решения так:

Ожидаемая полезность выбора двух коробок согласно EDT

Ожидаемая полезность выбора одной коробки согласно EDT

Согласно этим вычислениям, у выбора одной коробки ожидаемая полезность выше, так что EDT-агент одну коробку и выберет.

С другой стороны, учитывая, что решение агента каузально не повлияет на сделанное ранее предсказание Омеги, CDT-агент будет использовать одну и ту же вероятность, независимо от действия. Предпочитаемое в итоге решение будет одно и то же, независимо от этой вероятности, так что для иллюстрации мы просто произвольно положим вероятность, что в коробке ничего нет, равной 0.5, и, соответственно, вероятность, что в коробке миллион – тоже равной 0.5. Тогда CDT вычисляет ожидаемую полезность каждого решения так:

Ожидаемая полезность выбора двух коробок согласно CDT

Ожидаемая полезность выбора одной коробки согласно CDT

Согласно этим вычислениям, выбор двух коробок принесёт большую ожидаемую полезность, так что CDT-агент так и сделает. Там мы формальнее продемонстрировали ранее полученный неформально результат: в задаче Ньюкомба CDT-агенты будут брать две коробки, а EDT-агенты – одну.

Как уже упоминалось, есть и альтернативные формализации CDT. Вот Дэвид Льюис (1981) и Брайян Скайрмс (1980) предлагают подходы, которые полагаются на разделение мира на состояния, чтобы уловить каузальную информацию, а не на гипотетические условия. Например, в версии Льюиса, агент вычисляет ожидаемую полезность действий через безусловное отсылание к состояниям мира – гипотезам зависимости – описаниям того, как мир может отреагировать на действия. Они по сути своей содержат необходимую каузальную информацию.

Некоторые другие традиционные подходы к CDT: через визуализации из Собеля (1980) (ещё см. Льюис (1981)) и через безусловные ожидания из Сэвиджа (1954). Заинтересовавшимся в разных подходах к CDT лучше всего ознакомиться с Льюисом (1981), Вайрихом (2008), и Джойсом (1999). Из более нового: работы из области информатики над так называемыми каузальными байесовскими сетями привели е инновационному подходу к CDT, который получил некоторое недавнее внимание в философских изданиях (Перл 2000, гл. 4 и Спон (2012)).

Теперь, вооружившись EDT и формулировкой CDT через контрфактуалы, вернёмся к анализу сценариев с принятием решений.

11.1.3. Медицинские задачи Ньюкомба

Есть много вариантов медицинских задач Ньюкомба, но форма у них схожая. Есть, например, задача Соломона (Гиббард и Харпер (1976)) и задача о вреде курения (Иган (2007)). Ниже я опишу вариант под названием «задача о жвачке» (Юдковский (2010)):

Допустим, недавно опубликованное медицинское исследование показало, что жвачка, кажется, вызывает абсцесс горла. Исследователи обнаружили, что из людей, которые жуют жвачку, 90% умерло от абсцесса горла до 50 лет, а в то же время, из людей, которые жвачку не жуют – только 10%. Объясняя результаты, исследователи предположили, что слюна, протекая по горлу, портит клеточную защиту от бактерий. Жевали бы вы жвачку, прочитав это исследование? Но вот выходит другое исследование, оно показывает, что у большинства тех, кто жуёт жвачку, есть определённый ген, CGTA, и смертность укладывается в такую таблицу:

	CGTA есть	CGTA нет
Жуют жвачку	89% умирает	8% умирает
Не жуют жвачку	99% умирает	11% умирает

По ней получается, что есть у вас ген CGTA или нет, жвачка снижает ваши шансы умереть от абсцесса горла. Но почему тогда у тех, кто жуёт, настолько больше жертв? Потому что люди с геном CGTA склонны и жевать жвачку, и умирать от абсцесса. Авторы второго исследования продемонстрировали и эксперимент, показавший, что слюна от жевания жвачки может убивать бактерий, из-за которых образуется абсцесс. Исследователи предположили, что так как люди с геном CGTA сильно подвержены абсцессу горла, в ходе естественного отбора у них выработалась склонность жевать жвачку, чтобы защититься от абсцесса. Сильная корреляция между жеванием жвачки и абсцессом тогда вызвана не тем, что жвачка – причина абсцесса, а потому, что третий фактор – GCTA, приводит и к тому, и к другому.

Теперь, узнав об этом новом исследовании, вы бы выбрали жевать жвачку? Это защищает от абсцесса независимо от того, есть ли у вас ген CGTA. Но друг, узнавший, что вы решили жевать жвачку (как часто делают люди с геном CGTA) был бы очень обеспокоен этой новостью – так же, как новостью, что вы взяли обе коробки в задаче Ньюкомба. Кажется, в этом случае уже EDT выдаёт неправильный ответ. Это ставит под сомнение… правило «Выбирай такие действия, что ты был бы рад получить новость о том, что ты их выбрал». Хоть новость о том, что кто-то решил жевать жвачку и тревожит, но это всё равно защищает от абсцесса горла. Правило [CDT] «Выбирай такие действия, от которых ты ожидаешь позитивного воздействия на мир», кажется, сработает тут лучше.

Один из ответов на это, так называемая «защита от импульса» (tickle defense) (Иллс, 1981), возражает, что на самом деле EDT в таких случаях приходит к правильному ответу. Согласно этой защите, самый разумный способ сконструировать такую «задачу о жвачке» допускает, что CGTA вызывает желание («импульс»), из-за которого агент с большей вероятностью будет жевать жвачку, а не вызывает действие напрямую. Тогда, если мы допустим, что агент уже знает о своих желаниях, агент уже знает, вероятно ли, что у него есть ген CGTA, и выбор жевать жвачку не даст ему дополнительных плохих новостей. Следовательно, EDT-агент будет жевать жвачку, чтобы получить хорошую новость о том, что он уменьшил свои шансы абсцесса.

К сожалению, защита от импульса не достигает своих целей. Вводя этот подход, Иллс надеялся, что так EDT сможет подражать CDT без якобы неэлегантного полагания на каузальность. Но Собель (1994, гл. 2) показал, что защита от импульса с этим не справляется. И тех, кто чувствует, что EDT, выбирая одну коробку, правильно справлялась с задачей Ньюкомба, разочарует, что защита от импульса приводит к тому, что в некоторых версиях задачи Ньюкомба агент берёт две коробки. Так что она решает для теории одну проблему, но вводит другую.

Итак, так же, как CDT «проигрывает» в задаче Ньюкомба, EDT «проигрывает» в медицинских задачах Ньюкомба (если отвергнуть защиту от импульса) или же присоединяется к CDT и «проигрывает» в самой задаче Ньюкомба (если защиту от импульса принять).

11.1.4. Газировка Ньюкомба

Можно привести и другие проблематичные для EDT примеры, когда свидетельство, которое предоставляет ваше решение, касается не черты, с которой вы родились (или были созданы), а с какой-нибудь другой деталью мира. Один из таких примеров – задача про газировку Ньюкомба, придуманная Юдковским (2010):

Вы знаете, что в ходе двойного слепого клинического тестирования вам скоро дадут одну из двух газировок. После того, как вы её выпьете, вы войдёте в комнату, где будет шоколадное мороженое и ванильное мороженое. Первая возможная газировка производит сильное, но полностью подсознательное желание съесть шоколадное мороженое, а вторая – сильное подсознательное желание съесть ванильное мороженое. «Подсознательное» тут означает, что у вас нет интроспективного доступа к этому изменению, так же, как вы не можете отвечать на вопросы о работе отдельных нейронов вашего мозга. Вы можете лишь сделать вывод о своих изменившихся вкусах исходя из того, какое мороженое вы выбрали.

Все участники исследования, которые тестировали «шоколадную» газировку, будут после окончания исследования вознаграждены миллионом долларов, а те, кто тестировал «ванильную» газировку не получат ничего. Но, независимо от этого, подопытные, которые съели ванильное мороженое, получат дополнительную тысячу долларов, а те, кто съел шоколадное – никакой дополнительной выплаты. Псевдослучайный алгоритм поровну (50/50) распределяет подопытных между «шоколадной» и «ванильной» газировок. Вам известно, что 90% из тех предыдущих подопытных, которые съели шоколадное мороженое, действительно пили «шоколадную» газировку. И наоборот, 90% из тех предыдущих подопытных, которые съели ванильное мороженое, пили «ванильную» газировку. Какое мороженое вы бы съели?

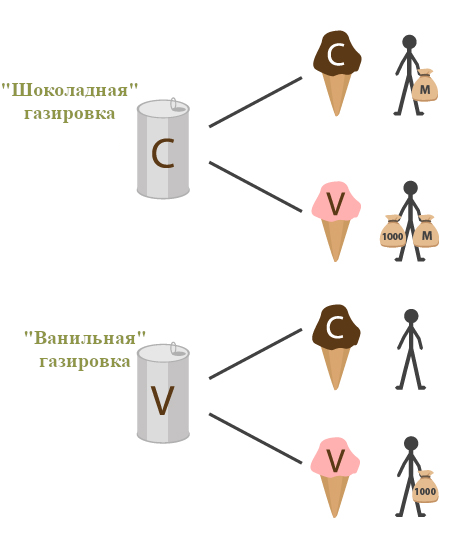
Газировка Ньюкомба

В этом случае EDT-агент решит съесть шоколадное мороженое, потому что это даст ему свидетельство в пользу того, что он выпил «шоколадную» газировку и после эксперимента получит миллион долларов. Но это кажется ошибочным решением, так что EDT-агент «проигрывает».

11.1.5. Мета-ньюкомбова задача Бострома

В ответ на нападки на их теорию, сторонники EDT могут представлять другие сценарии, в которых EDT «выигрывает», а как раз CDT «проигрывает». Один из таких примеров – Мета-ньюкомбова задача, предложенная Бостромом (2001). Если её подогнать к той же истории про суперинтеллектуального робота Омегу (раздел 11.1.1), она выглядит так: Либо Омега уже положил в коробку B миллион или ничего (в зависимости от своего предсказания вашего выбора), либо же Омега смотрит, как вы выбираете, и после этого кладёт или не кладёт миллион в зависимости от выбора. Но вы не знаете, что из этого правда. Примерно в половине случаев Омега делает свой ход перед игроком-человеком, а в половине – после него.

Но предположим, что есть другой суперинтеллектуальный робот, Мета-Омега, который, как известно, умеет идеально предсказывать как действия людей, так и действия Омеги. Мета-Омега говорит вам, что либо вы возьмёте две коробки, а Омега «сделает свой ход» после вашего выбора, либо вы возьмёте одну коробку, но Омега уже сделал свой ход (и улетел играть с кем-то ещё).

EDT-агент в таком случае берёт одну коробку и уходит с миллионом долларов. А вот CDT-агент сталкивается с дилеммой: если взять две коробки, кто действие Омеги зависит от выбора агента, так что «рационально» было бы взять одну коробку. Но если CDT-агент берёт одну коробку, то действие Омеги было раньше (а значит, физически не зависело от) выбора агента, так что «рациональным» решением было бы взять две коробки. Так что может показаться, что CDT-агент тут не сможет достичь какого бы то ни было решения. Но дальнейшее обдумывание выявляет, что тут всё сложнее. Согласно CDT, то, что агент должен сделать в этой ситуации, зависит от мнения агента в собственных действиях. Если у агента есть сильная уверенность, что он возьмёт две коробки, то он должен брать одну, а если у агента есть сильная уверенность, что он возьмёт одну коробку, то он должен брать две. Раз мнение агента о своих действиях не дано в условии это задачи, то сценарий недоопределён, и сложно сказать, какие выводы надо из него делать.

11.1.6. Кнопка психопата

Есть и другой случай, в котором, согласно CDT, то, что агент должен сделать, зависит от его мнения о том, что он сделает. Это представленная Иганом (2007) кнопка психопата:

Пол обдумывает, нажать ли кнопку «убить всех психопатов». Он думает, было бы куда лучше жить в мире без психопатов. К сожалению, Пол весьма уверен, что такую кнопку нажал бы только психопат. Пол очень сильно предпочитает жить в мире с психопатами по сравнению с тем, чтобы погибнуть. Должен ли Пол нажать кнопку?

Многие считают, что не должен. В конце концов, если он нажмёт, то он почти наверняка психопат, так что нажатие кнопки его убьёт. EDT-агент ответил бы так же: Нажатие кнопки сообщает агенту плохую новость, что он психопат, так что погибнет в результате своего действия.

С другой стороны, если Пол сильно уверен, что он не психопат, то CDT скажет, что он должен нажать на кнопку. CDT отметит, что, с учётом уверенности Пола, что он не психопат, его действия почти наверняка произведут положительный эффект – все психопаты умрут, а Пол выживет. Таким образом, CDT-агент тут решил бы неуместно и нажал бы кнопку. Важно заметить, что, в отличие от Мета-ньюкомбовой задачи, мнение о собственном поведении в полной версии этого сценария у Игана указано (не численно, агент думает, что вряд ли он психопат и, следовательно, вряд ли нажмёт кнопку).

Но, чтобы поставить для CDT такую задачу, Иган совершил несколько допущений о том, как агенту следует решать, что делать, в зависимости от того, что он думает, что он сделает. В ответ выдвигались альтернативные взгляды на то, как решать в таких ситуациях (в частности у Арнцениуса (2008) и Джойса (2012)). В результате всего этого, нет единого мнения о том, действительно ли задача с кнопкой психопата для CDT проблематична.

11.1.7. Автостопщик Парфита

Не все сценарии с принятием решений проблематично лишь для одной из CDT и EDT. Можно продемонстрировать и ситуации, в которых «проигрывают» как EDT-агент, так и CDT-агент. Один из таких примеров – Автостопщик Парфита (Парфит (1984), стр. 7):

Предположим, я еду на машине по пустыне. Машина ломается. Вы – незнакомец, и единственный другой водитель поблизости. Я вас остановил, и предлагаю большое вознаграждение, если вы меня спасёте. Я не могу выдать его вам сейчас, но обещаю это сделать, когда доберусь домой. Теперь допустим, что я прозрачен – не могу никого обмануть. Я не могу убедительно врать. Меня всегда выдаёт тон голоса, смущение, или что-то ещё. Наконец, допустим, что я знаю о себе, что я эгоист. Если вы довезёте меня до дому, мне будет хуже, если я отдам вам обещанное вознаграждение. Поскольку я знаю, что я никогда не сделаю то, что сделает мне хуже, я знаю, что нарушу своё обещание. Так как я не могу убедительно врать, вы тоже это знаете. Вы не верите моему обещанию и оставляете меня в пустыне.

В этом сценарии агент «проигрывает», если потом отказывается отдать незнакомцу вознаграждение. Но откажутся и EDT-агенты, и CDT-агенты. В конце концов, в этот момент агент уже в безопасности, так что отдав вознаграждение, они и не получат хороших новостей о своей безопасности, и не приведут к ней. Получается, в этом случае обе теории «проигрывают».

11.1.8. Прозрачная задача Ньюкомба

Есть и другие случаи, когда «проигрывают» и EDT, и CDT. Один из них – Прозрачная задача Ньюкомба, как минимум одна из её версий предложена у Дрешера (2006, стр. 238-242). Этот сценарий аналогичен изначальной задаче Ньюкомба, но в этом случае обе коробки прозрачные, так что вы видите их содержимое, когда принимаете решение. И опять Омега положил в коробку A тысячу долларов, а в коробку B – либо миллион, либо ничего, в зависимости от того, как Омега предсказал ваше поведение. Конкретнее, Омега предсказывал, как вы поступите, если увидите, что в коробке B лежит миллион. Если Омега предсказал, что вы возьмёте одну коробку, то он положил в коробку B миллион. А вот если Омега предсказал, что вы возьмёте обе коробки, то он не оставил коробку B пустой.

Как EDT-агенты, так и CDT-агенты в таком случае возьмут две коробки. В конце концов, содержимое коробок уже определено и известно, так что решение агента и не станет причиной чего=-то желаемого, и не даст об этом хороших новостей. Как и с выбором двух коробок в оригинальной задаче Ньюкомба, многие философы такое поведение одобряют.

Но стоит заметить, что Омега почти наверняка предсказал это решение и оставил коробку B пустой. CDT-агенты и EDT-агенты – все они уйдут с тысячей долларов. С другой стороны, как и в оригинальном случае, агент, который берёт одну коробку, получает миллион. Так что это тоже случай, в котором как «проигрывает» как EDT, так и CDT. Следовательно, для тех, кто согласен с комментариями (из раздела 11.1.1), что теория принятия решений не должна приводить к «проигрышу» агента, обе теории оказываются неудовлетворительными.

11.1.9. Контрфактуальное ограбление

Другой схожий случай, известный, как контрфактуальное ограбление, из Несова (2009):

Представьте, что однажды к вам приходит Омега и говорит, что он только что подбросил честную монетку, и, так как она упала решкой, он просит вас дать ему сто долларов. Согласитесь вы или нет, никаких дополнительных последствий не будет. Конечно, вы не хотите отдавать свои деньги. Но подождите, Омега говорит ещё и что если бы монетка упала орлом, то он отдал бы вам десять тысяч долларов, но только если он предсказал, что вы отдадите ему сто долларов, если монетка упадёт решкой.

Следует ли вам отдавать ему сто долларов?

И CDT, и EDT говорят, что нет. В конце концов, если вы отдадите свои деньги, это и не будет хорошими новостями, и не повлияет на ваши шансы получить десять тысяч. Да и интуитивно это кажется правильным решением. Так что в этом случае уместно оставить свои деньги себе..

Но, если допустить, что Омега идеально честен и достоин доверия, то, кажется, с этим заключением можно и поспорить. Если вы – такой агент, который при контрфактуальном ограблении отдаёт сто долларов, то вы в среднем будете получать лучшие результаты, чем агент, который не отдаёт. Конечно, в данном конкретном случае вы проиграете, но рациональные агенты вполне могут проигрывать в конкретных случаях (например, когда такой агент проигрывает рациональную ставку). Можно сказать, что рациональному агенту не следует быть таким агентом, который в среднем проигрывает. Агенты, которые отказываются отдавать сто долларов – это такие агенты, которые в среднем проигрывают. Так что, кажется, можно утверждать, что контрфактуальное ограбление – это ещё один случай, в котором неправильно действуют как CDT, так и EDT.

11.1.10. Дилемма заключённого

Перед тем, как перейти к более подробному обсуждению разных возможных теорий принятия решений, рассмотрим ещё один сценарий: дилемму заключённого. Резник (1987, стр. 147-148 ) так описывает этот сценарий:

Двух заключённых… арестовали за вандализм и изолировали друг от друга. Улик достаточно, чтобы вынести обвинительное заключение обоим, но прокурор хочет большего. Он подозревает, что они вместе ограбили банк, и он может получить от них признание в этом. Он допрашивает их по отдельности, и каждому говорит: «Я собираюсь предложить ту же сделку твоему товарищу, и я дам каждому из вас час на раздумья, а потом спрошу решение. Сделка такая: если один из вас признается в ограблении, а второй нет, то я обеспечу, чтобы тот, кто признался, получил год заключения, а другой – двадцать пять. Если вы признаетесь оба, то будет по десять лет каждому. Если никто из вас не признается, то я смогу посадить вас на два года по обвинению в вандализме…»

Матрица принятия решения для каждого заключённого такая:

	Товарищ признался	Товарищ солгал
Признаться	10 лет в тюрьме	1 год в тюрьме
Солгать	25 лет в тюрьме	2 года в тюрьме

Столкнувшись с таким сценарием CDT-агент признается. В конце концов, решение агента не может повлиять на решение товарища (их же изолировали друг от друга), так что агенту лучше, если он признается, независимо от того, что сделает товарищ. Согласно большинству исследователей теории принятия решений (и теории игр), признаться тут – действительно рациональное решение.

Но, несмотря на это, EDT-агент может соврать в дилемме заключённого. Конкретнее: если он думает, что товарищ достаточно похож на него самого, то агент соврёт, потому что это предоставит ему хорошую новость о том, что они оба соврут, а значит, ограничатся двумя годами тюрьмы (хорошая новость в сравнении с плохой новостью, что они оба признаются и получат десять лет тюрьмы).

Многим такой ход рассуждений кажется убедительным. Например Дуглас Хофштадтер (1985, стр. 737-780) утверждал, что агент, действующий «суперрационально» будет кооперировать с другими суперрациональными агентами ровно по этой причине: суперрациональный агент примет во внимание, что другие подобные агенты пройдут в ходе дилеммы заключённого через такой же мыслительный процесс, так что примут то же решение. В таком случае, лучше, чтобы решением обоих агентов было соврать, а не признаться. И в целом, можно сказать, что рациональному агенту в дилемме заключённого следует врать, если он считает, что достаточно похож на своего товарища, чтобы они пришли к одинаковому решению.

Аргумент в пользу кооперации в дилемме заключённого

Так что не вполне ясно, что именно стоит вывести из дилеммы заключённого. Но для тех, кто симпатизирует точке зрения Хофштадтера или рассуждениям EDT-агента, это очередная причина искать альтернативу для CDT.

11.2. Теория Бенчмарков (Benchmark theory, BT)

Один из недавних ответ на явную неспособность EDT справиться с медицинской задачей Ньюкомба, а CDT – с кнопкой психопата, это Теория Бенчмарков (BT), придуманная Вегвудом (2011) и развитая Бриггс (2010).

Простым языком можно описать этот алгоритм принятия решений так: агентам следует принимать решения так, чтобы предоставлять будущим версиям себя хорошие новости о том, насколько они хорошо справились по сравнению с другими возможными исходами. Если формально, BT использует для вычисления ожидаемой полезности действия A_i такую формулу:

Другими словами, она использует условные вероятности как EDT, но иначе вычисляет ценность (что показано использованием V’ вместо V). V’ вычисляется относительно значения-бенчмарка и предоставляет сравнительную меру ценности (оба источника выше разъясняют это подробнее).

Если говорить неформально, в задаче о жвачке BT отметит, что если агент будет жевать жвачку, то агент всегда получит хорошие новости о том, что у него всё сравнительно лучше, чем могло бы быть (потому что жвачка защищает его от абсцесса), а если не жевать, то плохие новости о том, что у него всё могло бы быть лучше, если бы он жевал. Так что BT-агент в этом сценарии будет жевать жвачку.

Кроме этого, BT достигает того, что, кажется, большинство считает правильным решением в задаче о кнопке психопата. Тут BT-агент заметит, что нажав кнопку он получит плохие новости о том, что он почти наверняка психопат и ему было бы сравнительно лучше не нажимать (потому что нажатие кнопки его убьёт). С другой стороны, если он не нажмёт, то он получит менее плохие новости о том, что он мог бы справиться немного лучше, нажав кнопку (потому что это убило бы всех психопатов, но не его самого). Так что отказ от нажатия кнопки даёт менее плохие новости, и это и есть рациональное решение.

Так что кажется, что есть неплохие причины считать BT убедительной: она хорошо справляется с сценариями, в которых, согласно некоторым людям, EDT и CDT хоть в одном да ошибаются.

К сожалению, BT-агент всё равно проваливается в других сценариях. Во-первых, те, кто считает взятие одной коробки правильным решением задачи Ньюкомба, сразу найдут в BT недостаток. в этом сценарии взятие двух коробок даёт хорошие новости о том, что агент справился сравнительно лучше, чем мог бы (потому что получил на тысячу долларов из коробки A больше, чем получил бы, приняв другое решение), а взятие одной коробки даёт плохие новости о том, что агент справился хуже, чем мог бы (потому что тех же денег не получил). Так что BT-агент в задаче Ньюкомба возьмёт две коробки.

Более того, Бриггс (2010) утверждает, что BT страдает и от других проблем, хоть Вегвуд (2011) это и отрицает. Так что даже для тех, кто поддерживает выбор двух коробок в задаче Ньюкомба, есть аргументы в пользу того, что BT – не лучшая теория выбора. Так что неясно, представляет ли BT достойную замену альтернативным теориям.

11.3. Вневременная теория принятия решений (Timeless decision theory, TDT)

Юдковский (2010) предложил другой алгоритм принятия решений, вневременную теорию принятия решений или TDT (см. также Altair, 2013). TDT конкретно предназначена соответствовать идее о том, что теория рационального выбора должна помогать агенту «выигрывать». Так что она привлекательна для тех, кто считает, что в задаче Ньюкомба надо брать одну коробку, а в задаче о жвачке жевать.

Простыми словами этот алгоритм можно приблизительно описать так: агент должен выбирать, как если права CDT, но он определяет не своё решение, а результат абстрактного вычисления, одной конкретной реализацией которого является его решение. Формализация этого алгоритма принятия решений занимает собственный документ немаленького размера, так что тут мы не будем её приводить полностью. Если же кратко, TDT строится поверх каузальных байесовский сетей (Перл, 2000) – графов, где направление рёбер соответствует каузальному влиянию. TDT расширяет эти графы, добавляя больше вершин, соответствующих абстрактным вычислениям. TDT принимает за объект выбора абстрактное вычисление, определяющее решение агента, а не само конкретное решение (см. более подробное описание у Юдковского, 2010).

Вернёмся к неформальному обсуждению. Прояснить TDT может помочь такой пример: представьте, что две точные копии человека поместили в одинаковые комнаты и поставили перед ними одинаковые выборы. Каждая копия совершает своё собственное решение, но они при этом совершают один и тот же процесс вычислений. Поэтому TDT говорит, что копиям следует действовать так, как будто они определяют результат этого процесса, а следовательно – поведение обеих копий.

Что-то аналогичное происходит и в задаче Ньюкомба. В ней почти что есть копия агента: внутренняя модель агента, которой пользуется омега, чтобы предсказать поведение агента. Изначальный агент, и эта «копия» используют один и тот же вычислительный процесс. Другими словами, этот процесс влияет как на предсказание Омеги, так и на поведение агента. Поэтому, TDT советует агенту действовать так, как если бы он определял результат этого процесса, а следовательно – как если бы он мог определить поведение Омеги при наполнении коробок. Поэтому TDT-агент возьмёт одну коробку, чтобы определить результат этого абстрактного вычисления таким, который приводит к миллиону долларов в коробке B.

TDT преуспевает и в других случаях. Например, в задаче о жвачке нет «копии» агента, так что TDT в этом случае действует так же, как обычная CDT и решает жевать жвачку. Дальше, в дилемме заключённого TDT-агент будет лгать, если его товарищ – другой TDT-агент (или достаточно похожий агент). В конце концов, в этом случае оба агента реализуют один и тот же вычислительный процесс, так что TDT советует агенту действовать так, как будто он определяет результат этого процесса, а следовательно – одновременно определяет своё решение и решение товарища. В таком случае для агента лучше, если они оба солгут, чем если они оба признаются.

Но, несмотря на эти успехи, TDT тоже «проигрывает» в некоторых сценариях принятия решений. Например, в контрфактуальном ограблении TDT-агент решит не отдавать сто долларов. Это может показаться удивительным. Казалось бы, как и в задаче Ньюкомба, тут Омега предсказывает поведение агента, а значит тут есть «копия». Но этот случай отличается тем, что агент знает, что монетка уже упала решкой, так что, отдав деньги, он ничего не получит.

Получается, что для тех, кто чувствует, что теория рационального выбора должна помогать агенту «выигрывать», TDT кажется шагом в правильном направлении. Но для того, чтобы «выигрывать» всегда, требуется дальнейшая работа.

11.4. Теория принятия решений и «выигрывание»

В предыдущем разделе я описал TDT, алгоритм принятия решений, который можно рассматривать как замену CDT и EDT. Одна из основных мотиваций для разработки TDT – ощущение, что как CDT, так и EDT в некоторых сценариях терпят неудачу. Но многие (пожалуй, даже большинство) исследователей теории принятия решений поддерживают CDT, хоть и признают, что CDT-агенты получают худший результат в Задаче Ньюкомба. Это может навести на мысль, что эти исследователи не заинтересованы в разработке алгоритма принятия решений, который бы «выигрывал», и у них какая-то другая цель. Если так, это ставит под сомнение ценность разработки алгоритмов, которые берут одну коробку.

Но утверждение о том, что большинство исследователей не интересуется тем, чтобы алгоритм «выигрывал», неправильно описывает их позицию. В конце концов, сторонники CDT обычно всерьёз воспринимают вызов, поставленный тем, что CDT-агенты «проигрывают» в Задаче Ньюкомба (в философской литературе это часто называют проблемой «Почему ты не богатый?»). Типичная реакция на этот вызов хорошо описана у Джойса (1999, стр. 153-154 ) как ответ на гипотетический вопрос о том, почему, если брать две коробки – рационально, CDT-агент в итоге получается менее богатым, чем агент, который берёт одну коробку:

У Рейчел есть совершенно замечательный ответ на «Почему ты не богатая?». «Я не богатая», скажет она, «потому что я – не такой человек, который [по мнению Омеги]» откажется от денег. Я попросту не такая, как ты, Ирен [выбирающая одну коробку]. С учётом того, что я знаю, что я – такой человек, который берёт деньги, и с учётом того, что [Омега] тоже это знает, для меня вполне разумно считать, что миллиона [в коробке] нет. Тысяча – максимум, который я могла получить, что бы я ни делала. Так что единcтвенным разумным вариантом для меня было бы её и взять.»

Ирен тут может попробовать продавить, спросив: «Но Рейчел, не хотела бы ты быть больше похожей на меня?»… Рейчел может, и ей следует, признать, что она хотела бы быть больше похожей на Ирен… после этого, Ирен воскликнет: «Ты признала это! Брать деньги, в конце концов, было не так уж и умно.» К сожалению Ирен, её заключение не следует из предпосылки Рейчел. Рейчел терпеливо объяснит, что хотеть быть человеком, который выбирает одну коробку, вполне совместимо с тем, чтобы считать, что надо брать тысячу долларов, независимо от того, какой ты человек. Когда Рейчел жалеет, что она не того же типа, что Ирен, она жалеет, что у неё нет тех вариантов, что у Ирен, а не поддерживает её выбор… Человек, который знает, что столкнётся (уже столкнулся) с задачей Ньюкомба, может хотеть стать (жалеть, что не был) таким человеком, которого [Омега] отметит, как берущего одну коробку. Это даёт повод (до [того, как коробки наполнены]) попробовать изменить свой тип, если это может поволиять на предсказание [Омеги]. Но это не даёт повода делать что-то, кроме как брать деньги, когда это уже не сможет повлиять на то, что сделал [Омега].

Другими словами, этот ответ проводит различие между выигрывающим решением и выигрывающим типом агентов, и заявляет, что брать две коробки в задаче Ньюкомба – выигрывающее решение, но при этом агенты, выбирающие одну коробку – выигрывающий тип агентов. Следовательно, пока теория принятия решений посвящена тому, какие решения рациональны, CDT в Задаче Ньюкомба рассуждает верно.

Для тех, кому этот ответ кажется странным, можно провести аналогию с задачей о жвачке. Почти все согласны, что в этом сценарии рациональное решение – жевать жвачку. Но статистически тем, кто не жуёт, лучше. Тогда не жующий может спросить: «Если ты такой умный, то почему не здоровый?». В этом случае описанный выше ответ особенно уместен. Те, кто жуёт, менее здоровы не из-за своего решения, а из-за того, что у них более вероятно есть нежелательный ген. Хорошие гены не делают не жующих более рациональными, только более везучими. Сторонник CDT попросту распространяет этот ответ и на Задачу Ньюкомба: те, кто выбирает одну коробку, богаты не из-за своего решения, а, скорее, из-за того, к какому типу агентов они относились, когда Омега наполнял коробки.

Стоит заметить одну последнюю деталь касательно этого решения. Сторонник CDT может соглашаться с этим аргументом, но всё равно признавать, что, при наличии возможности до наполнения коробок, было бы рационально модифицировать себя так, чтобы стать агентом, выбирающим одну коробку (как выше признаёт Джойс, и как утверждает Бёрджесс, 2004). Для сторонника CDT это вовсе не проблематично: если мы иногда вознаграждаемся не за рациональность решений в моменте, а за то, каким агентом мы были в какой-то момент в прошлом, то неудивительно, что сменить свой тип может быть выгодно.

На такую защиты выбора двух коробок в Задаче Ньюкомба есть разные ответы. Многие находят это убедительным, но другие, например, Ахмед и Прайс (2012) считают, что это не отвечает на вызов адекватно:

Каузалистское нытьё, что Задача Ньюкомба вознаграждает иррациональность, или, скорее, CDT-иррациональность, бесполезно. Суть аргумента – что если все знают, что CDT-иррациональная стратегия на самом деле в среднем достигает лучших результатов, чем CDT-рациональная стратегия, то пользоваться CDT-иррациональной стратегией рационально.

Получается, тут можно принять две позиции. Если ответ, данный сторонниками CDT, убедителен, то мы должны пытаться разработать теорию принятия решений, которая в Задаче Ньюкомба берёт две коробки. Возможно, CDT – лучшая теория для этой роли. Но, может, ещё лучше BT, которая, по мнению многих, лучше справляется с сценарием кнопки психопата. С другой стороны, если ответ сторонников CDT неубедителен, то нам надо разрабатывать теорию, которая в задаче Ньюкомба берёт одну коробку. В таком случае TDT, или что-то с ней схожее, кажется самым многообещающим вариантом из тех, что у нас есть.

[Прим. пер.: существуют ещё функциональная и несколько версий необновимой теории принятия решений (FDT и UDT соответственно). Насколько я понимаю, они идейно схожи с TDT, но, например, «выигрывают» в задачах про Автостопщика Парфита и про Контрфактуальное ограбление.]