Каузальные модели лежат в основе нашей работы. В этом посте мы представим краткое, но доступное объяснение каузальных моделей, которые могут описать вмешательства, контрфактуалы и агентов, что пригодится в следующих постах цепочки. Предполагается понимание основ теории вероятности, в частности – условных вероятностей.

Что такое каузальность?

Что значит, что из-за дождя трава стала зелёной? Тема каузальности философски любопытна и лежит в основе многих других важных для людей понятий. В частности, многие относящиеся к теме безопасности ИИ концепции вроде влияния, реакции, агентности, намерения, справедливости, вреда и манипуляции, сложно осмыслить без каузальной модели мира. Мы уже упоминали это в вводном посте и подробнее обсудим в следующих.

Вслед за Перлом мы примем определение каузальности через вмешательство: брызгалка сегодня каузально влияет на зелёность травы завтра, потому что если бы кто-то вмешался и выключил брызгалку, то зелёность травы была бы другой. Напротив, зелёность травы завтра не оказывает эффекта на брызгалку сегодня (предполагая, что вмешательство никто не предсказал). Так что брызгалка сегодня влияет на траву завтра, но не наоборот, как мы интуитивно и ожидаем.

Вмешательства

Каузальные Байесовские Сети (КБС) отображают каузальные зависимости между аспектами реальности при помощи ациклического ориентированного графа. Стрелка из переменной A в переменную B означает, что при сохранении значений остальных переменных A влияет на B. Например, нарисуем стрелку из брызгалки (S) к зелёности травы (G):

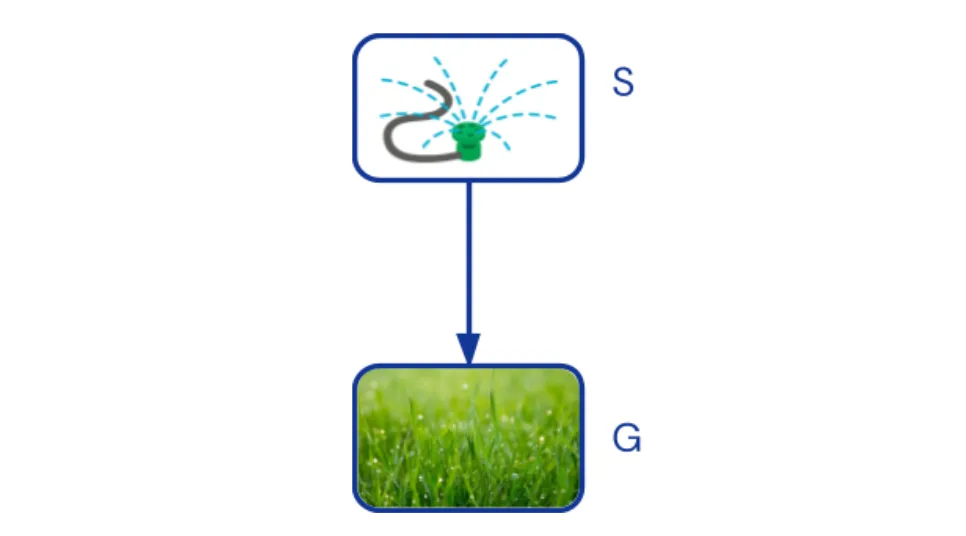
Каузальный граф, соответствующий нашему примеру. Брызгалка (S) влияет на зелёность травы (G).

У каждой вершины графа каузальный механизм того, как на него влияют его родительские узлы описывается условным распределением вероятностей. Для брызгалки распределение p(S) описыввет, как часто она включена, т.е. P(S=on)=30%. Для травы условное распределение p(G∣S) определяет, насколько вероятно, что трава станет зелёной, если брызгалка включена, т.е. p(G=green∣S=on)=100%, и если брызгалка выключена, т.е. p(G=green∣S=off)=30%.

Перемножая распределения мы получаем совместное распределение p(S,G)=p(S)p(G∣S), описывающее вероятность любой комбинации исходов. Совместные распределения – базовое понятие обычной теории вероятности. Их можно использовать, чтобы отвечать на вопросы вроде «какая вероятность, что брызгалка включена, при условии, что трава мокрая».

Вмешательство в систему меняет один или несколько механизмов каузальности. Например, вмешательство, которое включает брызгалку, соответствует замене механизма каузальности p(S) на новый механизм 1(S=on) – брызгалка всегда включена. Эффекты вмешательства можно выяснит, вычислив новое совместное распределение p(S,G∣do(S=on))=1(S=on)p(G|S), где do(S=on) обозначает вмешательство.

Заметим, что нельзя вычислить эффект вмешательства, зная только совместное распределение p(S,G), ведь без графа каузальности непонятно, надо ли менять механизм в разложении P(S)P(G∣S) или в inp(G)p(S∣G).

По сути, все статистические корреляции вызваны каузальным воздействием. [от переводчика: я тоже удивился этому тейку, можете посмотреть разъяснения в комментариях под оригинальным постом] Так что для набора переменных всегда есть какой-то КВБ, соответствующий каузальной структуре процесса, который генерирует данные. Впрочем, чтобы объяснить, например, неизмеренные факторы в нём могут потребоваться дополнительные переменные.

Контрфактуалы

Пусть брызгалка включена, а трава зелёная. Была бы трава зелёная, если бы брызгалка не была включена? Вопросы о гипотетических контрфактуалах сложнее, чем вопросы о вмешательствах, потому что для них надо думать о нескольких мирах. Контрфактуалы – ключ к определению вреда, намерения, справедливости и того, как измерять воздействие. Все эти понятия зависят от сравнения исходов с гипотетическими мирами.

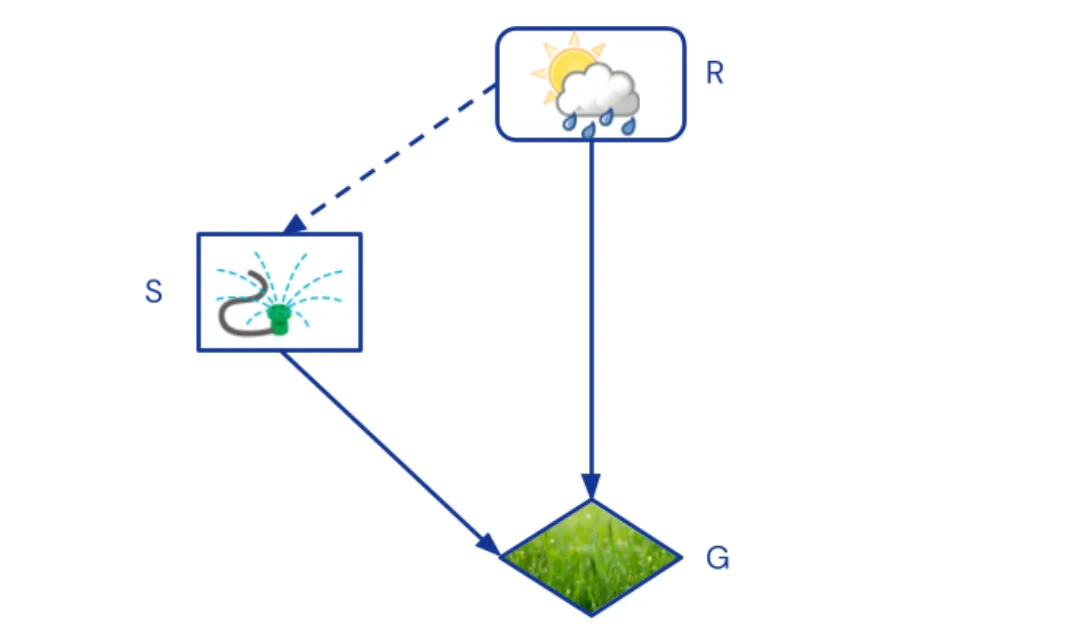
Чтобы справляться с такими рассуждениями, структурные каузальные модели (СКМ) добавляют к КБС три важных аспекта. Во-первых, общий для гипотетических миров фоновый контекст явно отделяется от переменных, в которые возможны вмешательства и которые в разных мирах могут отличаться. Первые называют экзогенными переменными, а вторые – эндогенными. В нашем примере полезно ввести экзогенную переменную R, обозначающую, идёт ли дождь. Брызгалка и зелёность травы – эндогенные переменные.

Отношения между гипотетическими мирами можно отобразить двойным графом, в котором есть по две копии эндогенных переменных – для настоящего мира и гипотетического и внешняя переменная/переменные, дающие общий контекст:

Граф, нужный, чтобы ответить, является ли брызгалка причиной того, что трава зелёная. Вершины из гипотетического мира обведены пунктиром. Правая вершина-брызгалка подвержена вмешательству do(S=off), что обозначает гипотетическую ситуацию. Серая внешняя вершина-дождь R даёт общий контекст.

Во-вторых, для СКМ вводится нотация для различия эндогенных переменных в разных гипотетических мирах. Например, G_S=off обозначает зелёность травы в гипотетическом мире, где брызгалка выключена. Можно считать это сокращением для «G∣do(S=off)» с тем преимуществом, что это можно вставлять в выражения с переменными из других миров. Например, наш вопрос можно сформулировать как p(G_S=off=green|S=on,G=green), где G_S=off=green – гипотетическая ситуация, а S=on,G=green – настоящие наблюдения.

В третьих, в СКМ требуется, чтобы у всех эндогенных переменных были детерминированные механизмы каузальности. В нашем случае это выполняется, если мы предполагаем, что брызгалка включена, когда дождя нет, а трава становится зелёной (только) тогда, когда идёт дождь или включена брызгалка.

Детерминизм означает, что перейти к условному распределению просто – надо лишь обновить распределение по экзогенным переменным, т.е. P(R) заменяется на P(R∣S=on,G=green). В нашем случае вероятность дождя снижается с 30% до 0%, потому что, если идёт дождь, брызгалка выключена.

Так что для ответа на наш вопрос надо произвести три шага рассуждения:

• Абдукция: заменить P(R) на P(R∣S=on,G=green)
• Вмешательство: выключить брызгалку, do(S=off)
• Предсказание: вычислить значение G в получившейся модели.

Или то же самое одной формулой:

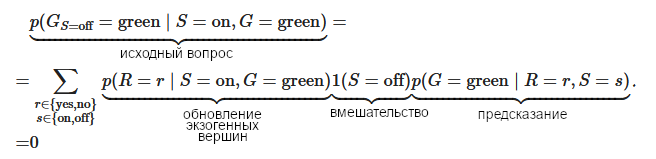
В итоге мы можем сказать, что если бы брызгалка была выключена, трава не была бы зелёной (при принятии наших допущений о взаимосвязях).

СКМ строго мощнее КБС. Их основной недостаток – они требуют детерминированных взаимосвязей между эндогенными переменными, а их на практике часто сложно определить. Ещё они ограничены контрфактуалами без отходов назад, гипотетическими мирами, которые отличаются исключительно вмешательствами.

Один агент

Пусть мы хотим вывести намерения или стимулы некоего Джона, или же предсказать, как его поведение подстроилось бы под изменения в его модели мира. Нам потребуется диаграмма каузальных воздействий (ДКВ), помечающая вершины-переменные как относящиеся к случайности, решениям или полезности. В нашем примере дождь был бы вершиной случайности, брызгалка – вершиной-решением, а зелёность травы – вершиной-полезностью. Раз дождь – родительская вершина брызгалки, значит, Джон наблюдает его перед тем, как решать, включать ли её. Графически будем обозначать случайности как раньше, решения прямоугольниками, а полезность ромбами. Заштрихованные рёбра означают наблюдения.

ДКВ, соответствующая нашему примеру. Включение или не включение брызгалки – решение, оптимизирующее зелёность травы.

Агент определяет каузальные механизмы своих решений, т.е. свою политику, с цель. максимизации суммы по своим вершинам-полезностям. В нашем примере оптимальной политикой было бы включить брызгалку, когда дождя нет (решение в случае дождя не имеет значения). Когда политика определена, ДКВ определяет КБС.

В моделях с агентами есть два вида воздействий, зависящих от того, адаптируют агенты под них свои политики или нет. Например, Джон сможет выбрать другую политику касательно брызгалки только если мы проинформируем его о вмешательстве до того, как он уже принял своё решение. Вмешательства до и после политики можно обрабатывать всё тем же оператором do, если мы добавим в модель так называемые вершины-механизмы. Больше о них будет в следующем посте.

Много агентов.

Взаимодействие нескольких агентов можно промоделировать каузальными играми. В них у каждого агента есть множества переменных-решений и переменных-полезностей.

Проиллюстрируем. Пусть Джон иногда засеивает новую траву. Птицам нравится клевать семена, но они не могут издалека понять, есть ли они там. Они могут лишь видеть, использует ли Джон брызгалку, а это вероятнее, когда трава новая. Джон хочет орошать свой газон, когда тот новый, но не хочет, чтобы птицы клевали семена. Вот структура этой сигнальной игры:

Каузальная игра, соответствующая нашему усложнённому примеру. Разные цвета означают решения и полезности разных агентов. Между новыми семенами (N) и птицами (B) нет ребра – птицы не могут их увидеть.

Помимо лучшего моделирования каузальности, у каузальных игр есть и другие преимущества над стандартной развёрнутой формой игр (РФИ). Например, каузальная игра сразу показывает, что птицам не важно, орошён газон или нет, ведь единственный путь от брызгалки S к еде F лежит через решение самих птиц B. В РФИ эта информация была бы скрыта в числах выигрыша. Каузальные игры более явно отображают независимость переменных, что иногда позволяет найти больше подигр и исключить больше ненадёжных угроз. При этом, каузальную игру всегда можно сконвертировать в РФИ.

Аналогично различиям между совместными распределениями, КБС и СКМ, есть (мультиагентные диаграммы воздействия, которые включают агентов в не обязательно каузальные графы, структурные каузальные модели воздействия и структурные каузальные игры, которые комбинируют агентов с экзогенными вершинами и детерминизмом, чтобы отвечать на вопросы о контрфактуалах.

Заключение

В этом посте мы ввели модели, которые могут отвечать на вопросы о корреляциях, вмешательствах и контрфактуалах с участием нуля, одного или нескольких агентов. В итоге есть девять возможных видов моделей. Более подробное введение в каузальные модели можно прочитать в Разделе 2 «Рассуждений о каузальности в играх» и книгу Перла «A Primer».

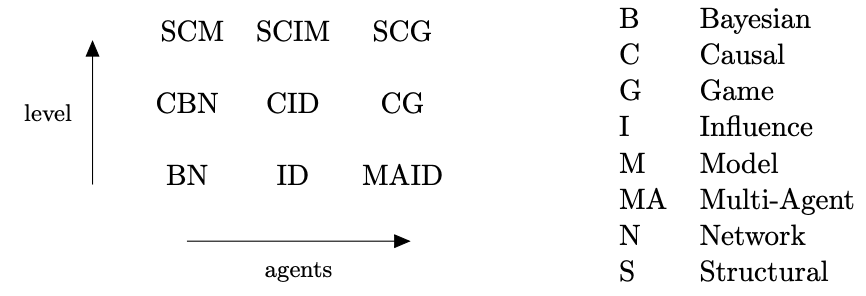
Таксономия каузальных моделей и их аббревиатуры. Вертикальная ось располагает модели по каузальной иерархии (ассоциативные, интервенционистские (с вмешательствами) и контрфактуальные), а горизонтальная – по количеству агентов (0, 1 и n).[от переводчика: в остатке цепочки эти аббревиатуры применяться не будут, так что я оставил схему без перевода]

В следующем посте мы будем использовать КИД и каузальные игры для моделирования агентов. Но что есть агент? В следующем посте мы попробуем лучше разобраться в этом, посмотрев на некоторые свойства, общие для всех агентных систем.